题目内容
17.已知圆锥的高为h,底半径为r,用我们计算抛物线下曲边梯形面积的思路,推导圆锥体积的计算公式.[提示:(1)用若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片;
(2)用一系列圆柱的体积近似地代替对应的薄片,圆柱的高为$\frac{h}{n}$,底半径顺次为:$\frac{r}{n}$,$\frac{2r}{n}$,$\frac{3r}{n}$…,$\frac{(n-1)r}{n}$,r;
(3)问题归结为计算和式V(n)=$\frac{h}{n}$×(12+22+…+n2)×$\frac{π{r}^{2}}{{n}^{2}}$,当n越来越大时所趋向的值.].
分析 利用极限的定义进行分割、近似代换和求极限的方法,进行推到
解答 解:(1)若干张平行于圆锥底面的平面把它切成n块厚度相等的薄片;
(2)用一系列圆柱的体积近似地代替对应的薄片,圆柱的高为$\frac{h}{n}$,底半径顺次为:$\frac{r}{n}$,$\frac{2r}{n}$,$\frac{3r}{n}$…,$\frac{(n-1)r}{n}$,r;
(3)问题归结为计算和式V(n)=$\frac{h}{n}$×(12+22+…+n2)×$\frac{π{r}^{2}}{{n}^{2}}$,当n越来越大时所趋向的值.
(对V求极限V=$\underset{lim}{n→∞}$$\frac{h}{n}$×(12+22+…+n2)×$\frac{π{r}^{2}}{{n}^{2}}$
=$\underset{lim}{n→∞}$$\frac{h}{n}•\frac{1}{6}n(n+1)(2n+1)•\frac{π{r}^{2}}{{n}^{2}}$
=$\frac{hπ{r}^{2}}{6}$$\underset{lim}{n→∞}$$\frac{2{n}^{2}+3n+1}{{n}^{2}}$
=$\frac{π{r}^{2}h}{3}$
=$\frac{1}{3}{S}_{底}h$
故圆锥的体积等于$\frac{1}{3}$的圆柱体的体积
点评 利用极限的思想对圆锥进行分割、近似代换和求极限,属于中档题.

练习册系列答案
相关题目
18.在平面直角坐标系中,一束光线从点M(-2,3)出发,被直线y=x-1反射后到达点N(1,6),则这束光线从M到N所经过的路程为( )
| A. | 10$\sqrt{3}$ | B. | 3$\sqrt{10}$ | C. | 2$\sqrt{10}$ | D. | 3$\sqrt{2}$ |
9.已知某大城市对每人车流量拥挤等级规定如表:
该城市对国庆节7天的车流量作出如下表的统计数据:
(1)某人国庆节连续2天到该城市游玩,求这2天他遇到的车流量拥挤等级均为严重拥挤的概率;
(2)从国庆节期间随机选取2天,记这2天该城市车流量拥挤等级不是“严重拥挤”的天数为X,求X的分布列及数学期望.
| 车流量(万辆) | 0~10 | 11~50 | 51~70 | 71~80 | 81~100 | >100 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |
| 日期 | 10月1日 | 10月2日 | 10月3日 | 10月4日 | 10月5日 | 10月6日 | 107日 |
| 车流量(万辆) | 120 | 110 | 85 | 75 | 60 | 105 | 110 |
(2)从国庆节期间随机选取2天,记这2天该城市车流量拥挤等级不是“严重拥挤”的天数为X,求X的分布列及数学期望.
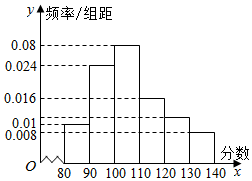 某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.
某校在2 015年11月份的高三期中考试后,随机地抽取了50名学生的数学成绩并进行了分析,结果这50名同学的成绩全部介于80分到140分之间.现将结果按如下方式分为6组,第一组[80,90),第二组[90,100),…第六组[130,140],得到如图所示的频率分布直方图.