题目内容
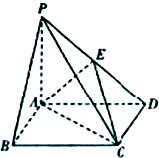 在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2
在四棱锥P-ABCD中,底面ABCD是矩形,PA=AD=4,AB=2,PB=2| 5 |
| 2 |
(1)PB∥平面ACE;
(2)求证:AE⊥平面PCD;
(3)求四面体PACE的体积.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,直线与平面垂直的判定
专题:综合题,空间位置关系与距离
分析:(1)连接BD,AC∩BD=0,则O是BD的中点,利用OE是中位线,所以PB∥OE.因为PB?平面ACE,OE?平面ACE,所以PB∥平面ACE;
(2)根据边的长度关系可知三角形PAD是等腰直角三角形,所以PA⊥AD,同理PA⊥AB,又AD∩AB=A,满足线面垂直的判断定理,则PA⊥平面ABCD,根据线面垂直得到面面垂直,再由面面垂直得到线线垂直,即CD⊥AE,因为E是PD的中点,三角形PAD是等腰直角三角形,从而AE⊥PD,又PD∩CD=D,满足线面垂直的判定定理可得结论.
(3)四面体PACE的体积为VA-PCE,即可求解.
(2)根据边的长度关系可知三角形PAD是等腰直角三角形,所以PA⊥AD,同理PA⊥AB,又AD∩AB=A,满足线面垂直的判断定理,则PA⊥平面ABCD,根据线面垂直得到面面垂直,再由面面垂直得到线线垂直,即CD⊥AE,因为E是PD的中点,三角形PAD是等腰直角三角形,从而AE⊥PD,又PD∩CD=D,满足线面垂直的判定定理可得结论.
(3)四面体PACE的体积为VA-PCE,即可求解.
解答:
(1)证明:连接BD,AC∩BD=0,则O是BD的中点,
因为E是PD的中点,
所以PB∥OE
因为PB?平面ACE,OE?平面ACE,
所以PB∥平面ACE;
(2)因为PA2+AD2=42+42=32,PD2=(4
)2=32,
所以三角形PAD是等腰直角三角形,所以PA⊥AD.
同理PA2+AB2=42+22=20,PB2=(2
)2=20,
所以三角形PAB是直角三角形,所以PA⊥AB.
又AD∩AB=A,所以PA⊥平面ABCD,
所以平面PAD⊥平面ABCD.
因为底面ABCD是矩形,所以CD⊥AD,
所以CD⊥平面PAD,
因为AE?平面PAD,
所以CD⊥AE.
因为E是PD的中点,三角形PAD是等腰直角三角形,
所以AE⊥PD.
又PD∩CD=D,所以AE⊥平面PCD.
(3)解:四面体PACE的体积为VA-PCE=
•
•2
•2•2
=
.
因为E是PD的中点,
所以PB∥OE
因为PB?平面ACE,OE?平面ACE,
所以PB∥平面ACE;
(2)因为PA2+AD2=42+42=32,PD2=(4
| 2 |
所以三角形PAD是等腰直角三角形,所以PA⊥AD.
同理PA2+AB2=42+22=20,PB2=(2
| 5 |
所以三角形PAB是直角三角形,所以PA⊥AB.
又AD∩AB=A,所以PA⊥平面ABCD,
所以平面PAD⊥平面ABCD.
因为底面ABCD是矩形,所以CD⊥AD,
所以CD⊥平面PAD,
因为AE?平面PAD,
所以CD⊥AE.
因为E是PD的中点,三角形PAD是等腰直角三角形,
所以AE⊥PD.
又PD∩CD=D,所以AE⊥平面PCD.
(3)解:四面体PACE的体积为VA-PCE=
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| 2 |
| 8 |
| 3 |
点评:证明线面平行只要在平面内找到一条直线与已知直线平行即可,证明面与面垂直只要证明其中一个平面过另一个平面的垂线即可,求三棱锥的体积关键是找到一个高并且简单易求.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
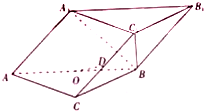 三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.
三棱柱ABC-A1B1C1中,平面A1ABB1⊥平面ABC,O是AB的中点.