题目内容
在直角坐标系里,设集合M={m|m是直线Ax+By=0,其中A2+B2≠0且A,B∈R},N={n|n是直线y=kx,其中k∈R},则集合M,N的关系是( )
| A、M=N | B、M⊆N |
| C、M?N | D、以上都不对 |
考点:直线的一般式方程,直线的斜截式方程
专题:直线与圆
分析:对B分类讨论,可得集合M表示的是经过原点的所有直线.而N表示的是经过原点但不包括y轴的所有直线.可得N?M.即可得出.
解答:
解:当B=0,A≠0时,直线Ax+By=0表示y轴;当B≠0时,直线Ax+By=0表示经过原点的一条直线.因此集合M表示的是经过原点的所有直线.
而N={n|n是直线y=kx,其中k∈R},表示的是经过原点但不包括y轴的所有直线.
∴N?M.
故选:C.
而N={n|n是直线y=kx,其中k∈R},表示的是经过原点但不包括y轴的所有直线.
∴N?M.
故选:C.
点评:本题考查了直线的方程、集合之间的关系,考查了分类讨论思想方法,属于基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
函数y=x(|x|-1)的图象是( )
A、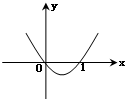 |
B、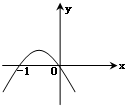 |
C、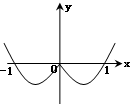 |
D、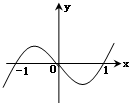 |