题目内容
已知点P(1,2,3),Q(-3,5,
),它们在面xoy内的射影分别是P′,Q′,则|P′Q′|= .
| 2 |
考点:空间两点间的距离公式,空间中的点的坐标
专题:空间位置关系与距离
分析:分别求出点P(1,2,3),Q(-3,5,
),在xoy内的射影P′,Q′的坐标,利用两点间的距离公式进行求解即可.
| 2 |
解答:
解:点P(1,2,3),Q(-3,5,
),在xoy内的射影P′,Q′的坐标分别为:
P′(1,2,0),Q′(-3,5,0),
则|P′Q′|=
=
=
=5,
故答案为:5
| 2 |
P′(1,2,0),Q′(-3,5,0),
则|P′Q′|=
| (-3-1)2+(5-2)2 |
| 16+9 |
| 25 |
故答案为:5
点评:本题主要考查空间两点间的距离公式的计算,求出射影坐标是解决本题的关键.

练习册系列答案
相关题目
如图所示的阴影部分﹙包括边界﹚对应的二元一次不等式组为( )
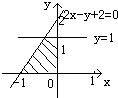
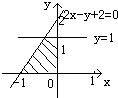
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
若有两个焦点F1,F2的圆锥曲线上存在点P,使|PF1|=3|PF2|成立,则称该圆锥曲线上存在“α”点,现给出四个圆锥曲线:①
-
=1 ②x2-
=1 ③
+
=1 ④
+
=1,其中存在“α”点的圆锥曲线有( )
| x2 |
| 4 |
| y2 |
| 12 |
| y2 |
| 15 |
| x2 |
| 9 |
| y2 |
| 7 |
| x2 |
| 12 |
| y2 |
| 4 |
| A、①③ | B、①④ | C、②③ | D、②④ |
设函数f(x)在(0,+∞)内可导,且f(ex)=x+ex,则f′(1)=( )
| A、1 | B、2 | C、3 | D、4 |
函数y=ln(2x-1)的定义域是( )
| A、[0,+∞) |
| B、[1,+∞) |
| C、(0,+∞) |
| D、(1,+∞) |
在直角坐标系里,设集合M={m|m是直线Ax+By=0,其中A2+B2≠0且A,B∈R},N={n|n是直线y=kx,其中k∈R},则集合M,N的关系是( )
| A、M=N | B、M⊆N |
| C、M?N | D、以上都不对 |
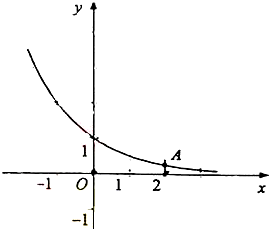 如图,函数f(x)=ax(a>0,a≠1)的图象经过点A(2,
如图,函数f(x)=ax(a>0,a≠1)的图象经过点A(2,