题目内容
设直线l的倾斜角为α，且
≤α≤
，则直线l的斜率k的取值范围是 ．
| π |
| 4 |
| 5π |
| 6 |
考点：直线的倾斜角
专题：直线与圆
分析：由已知得直线l的斜率k的取值范围是tan
≤k＜tan
或tan
＜k＜tan
，由此能求出结果．
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 6 |
解答：
解：∵直线l的倾斜角为α，且
≤α≤
，
∴直线l的斜率k的取值范围是：
tan
≤k＜tan
或tan
＜k＜tan
，
∴1≤k＜+∞或-∞＜k＜-
，
∴直线l的斜率k的取值范围是（-∞，-
]∪[1，+∞）．
故答案为：（-∞，-
]∪[1，+∞）．
| π |
| 4 |
| 5π |
| 6 |
∴直线l的斜率k的取值范围是：
tan
| π |
| 4 |
| π |
| 2 |
| π |
| 2 |
| 5π |
| 6 |
∴1≤k＜+∞或-∞＜k＜-
| ||
| 3 |
∴直线l的斜率k的取值范围是（-∞，-
| ||
| 3 |
故答案为：（-∞，-
| ||
| 3 |
点评：本题考查直线的斜率的取值范围的求法，是基础题，解题时要注意正切函数的性质的合理运用．
练习册系列答案
双基同步导航训练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
在直角坐标系里，设集合M={m|m是直线Ax+By=0，其中A2+B2≠0且A，B∈R}，N={n|n是直线y=kx，其中k∈R}，则集合M，N的关系是（ ）
| A、M=N | B、M⊆N |
| C、M?N | D、以上都不对 |
如图所示，直线l1，l2，l3的斜率分别为k1，k2，k3，则（ ）
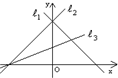
| A、k1＜k2＜k3 |
| B、k3＜k1＜k2 |
| C、k1＜k3＜k2 |
| D、k3＜k2＜k1 |
函数f（x）=
+lg（4-x）的定义域为（ ）
| ||
| x-3 |
| A、[2，+∞） |
| B、[2，3） |
| C、[2，4） |
| D、[2，3）或（3，4） |