题目内容
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
分析 设正△ABC的中心为O1,连结O1O、O1C、O1D、OD.根据球的截面圆性质、正三角形的性质与勾股定理,结合题中数据能求出结果.
解答 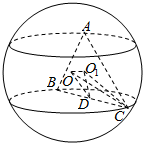 解:设正△ABC的中心为O1,连结O1O、O1C、O1D、OD,
解:设正△ABC的中心为O1,连结O1O、O1C、O1D、OD,
∵O1是正△ABC的中心,A、B、C三点都在球面上,
∴O1O⊥平面ABC,结合O1C?平面ABC,可得O1O⊥O1C,
∵边长为3的正三角形ABC中,O1C=$\frac{2}{3}\sqrt{{3}^{2}-(\frac{3}{2})^{2}}$=$\sqrt{3}$.
∵Rt△O1OC中,O1C=$\sqrt{3}$,OO1⊥O1C,球的半径OC=R=2,
∴球心O到平面ABC的距离O1O=$\sqrt{{R}^{2}-{O}_{1}{C}^{2}}$=$\sqrt{{2}^{2}-(\sqrt{3})^{2}}$=1.
故选:A.
点评 本题已知球的内接正三角形与球心的距离,求经过正三角形中点的最小截面圆的面积.着重考查了勾股定理、球的截面圆性质与正三角形的性质等知识,属于中档题.

练习册系列答案
相关题目
9.二面角α-l-β的大小为60°,A∈α,B∈β,且A、B两点在l上的射影分别为A′、B′,其中BB′=1,AA′=2,A′B′=3,点C是l上任一点,则AC+BC的最小值为( )
| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
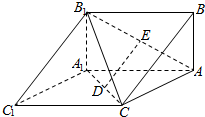 如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.
如图,三棱柱ABC-A1B1C1中,BA⊥平面AA1C1C,AB=2$\sqrt{2}$,AA1=AC=4,∠A1C1C=60°,D、E分别为A1C,AB1的中点.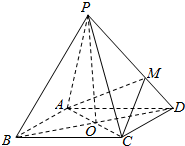 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,∠BCD=120°,M为侧棱PD的三等分点(靠近D点),O为AC,BD的交点,且PO⊥面ABCD,PC=2.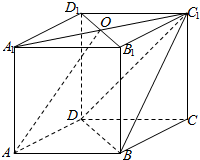 在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.
在四棱柱ABCD-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD为菱形,O为A1C1与B1D1的交点,已知AA1=AB=1,∠BAD=60°.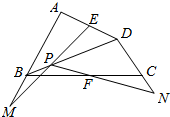 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.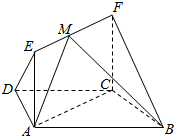 如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.
如图,矩形ACFE⊥底面ABCD,底面ABCD为等腰梯形,且AB∥CD,AB=2AD=2CD=2CF.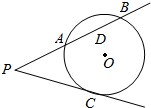 如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.
如图,过点P作圆O的切线PC,切点为C,过点P的直线与圆O交于点A,B(PA<PB),且AB的中点为D.