题目内容
9.二面角α-l-β的大小为60°,A∈α,B∈β,且A、B两点在l上的射影分别为A′、B′,其中BB′=1,AA′=2,A′B′=3,点C是l上任一点,则AC+BC的最小值为( )| A. | 4$\sqrt{2}$ | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 3$\sqrt{2}$ |
分析 画出图形,把二面角α-l-β展开为应该平面,然后求解AC+BC的最小值.
解答  解:如图:二面角α-l-β的大小为60°,A∈α,B∈β,且A、B两点在l上的射影分别为A′、B′,其中BB′=1,AA′=2,A′B′=3,点C是l上任一点,则AC+BC的最小值为展开的平面图形中AB的距离,AB=AC+BC=$\sqrt{{3}^{2}+{3}^{2}}$=$3\sqrt{2}$.
解:如图:二面角α-l-β的大小为60°,A∈α,B∈β,且A、B两点在l上的射影分别为A′、B′,其中BB′=1,AA′=2,A′B′=3,点C是l上任一点,则AC+BC的最小值为展开的平面图形中AB的距离,AB=AC+BC=$\sqrt{{3}^{2}+{3}^{2}}$=$3\sqrt{2}$.

故选:D.
点评 本题考查与二面角有关的几何问题,距离的最值的求法,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
 =(-8,1),
=(-8,1), =(3,4),则
=(3,4),则 方向上的射影是
方向上的射影是  ,则cos(α+
,则cos(α+ )=( )
)=( ) B.
B. C.
C. D.
D.
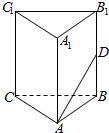 如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求:
如图所示,在正三棱柱ABC-A1B1C1中,已知AB=1,D是棱BB1上的点,且BD=1,求: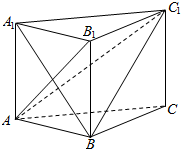 如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.
如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.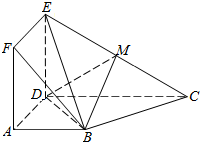 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=$\frac{1}{2}$CD=2,点M是线段EC的中点.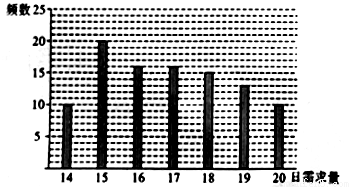
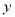 (单位:元)关于当天需求量
(单位:元)关于当天需求量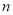 (单位:个,
(单位:个,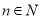 )的函数解析式;
)的函数解析式;