题目内容
18.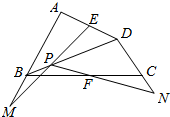 如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
如图,四边形ABCD中,E,F分别是AD,BC的中点,P是对角线BD上的一点,直线EP,PF分别交AB,DC的延长线于M,N.证明:线段MN被直线EF所平分.
分析 设EF∩MN=G,直线EF截△PMN,欲证G是线段MN的中点,只要证$\frac{PF}{NF}=\frac{PE}{ME}$,由此能证明线段MN被直线EF所平分.
解答  证明:设EF∩MN=G,直线EF截△PMN,
证明:设EF∩MN=G,直线EF截△PMN,
则$\frac{NG}{GM}•\frac{ME}{EP}•\frac{PF}{FN}$=1,
欲证G是线段MN的中点,只要证$\frac{PF}{NF}=\frac{PE}{ME}$,①
直线AB截△PDE,得$\frac{PM}{ME}•\frac{EA}{AD}•\frac{BD}{BP}$=1,即$\frac{MP}{2ME}=\frac{BP}{BD}$,②
直线CD截△PBF,则有$\frac{PN}{NF}•\frac{FC}{CB}•\frac{BD}{DP}$=1,即$\frac{NP}{2NF}=\frac{PD}{BD}$,③
②③相加,得$\frac{MP}{ME}+\frac{NP}{NF}=2$,即$\frac{NP}{NF}-1=1-\frac{MP}{ME}$,
即$\frac{PF}{NF}=\frac{PE}{ME}$,
∴线段MN被直线EF所平分.
点评 本题考查线段被直线平分的证明,是中档题,解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
相关题目
6.过点(2,-2)且以$y=±\frac{{\sqrt{2}}}{2}x$为渐近线的双曲线方程是( )
| A. | $\frac{y^2}{2}-\frac{x^2}{4}=1$ | B. | $\frac{x^2}{4}-\frac{y^2}{2}=1$ | C. | $\frac{y^2}{4}-\frac{x^2}{2}=1$ | D. | $\frac{x^2}{2}-\frac{y^2}{4}=1$ |
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
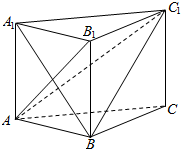 如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.
如图,三棱柱中ABC-A1B1C1,侧棱与底面ABC垂直,且AB1⊥BC1,AB=AA1=1,BC=2.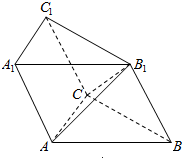 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.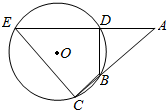 如图,⊙O的弦ED,CB的延长线交于点A.
如图,⊙O的弦ED,CB的延长线交于点A. 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD