题目内容
2.已知点A(4,1,3),B(6,3,2),且$\overrightarrow{AC}=3\overrightarrow{AB}$,则点C的坐标为(10,7,0).分析 设出C的坐标,根据条件列出方程解出.
解答 解:设C(a,b,c),则$\overrightarrow{AC}$=(a-4,b-1,c-3),$\overrightarrow{AB}$=(2,2,-1).
∵$\overrightarrow{AC}=3\overrightarrow{AB}$,∴$\left\{\begin{array}{l}{a-4=6}\\{b-1=6}\\{c-3=-3}\end{array}\right.$,解得$\left\{\begin{array}{l}{a=10}\\{b=7}\\{c=0}\end{array}\right.$.
故答案为(10,7,0).
点评 本题考查了空间向量的坐标运算,属于基础题.

练习册系列答案
相关题目
13.已知边长为3的正三角形ABC的三个顶点都在半径为2的球O的球面上,则点O到平面ABC的距离为( )
| A. | 1 | B. | $\frac{\sqrt{2}}{2}$ | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
14.函数f(x)在x=x0处导数存在,若p:f′(x0)=0;q:x=x0是f(x)的极值点,则p是q的( )
| A. | 充分不必要条件 | B. | 充要条件 | ||
| C. | 必要不充条件 | D. | 既非充分条件也非必要条件 |
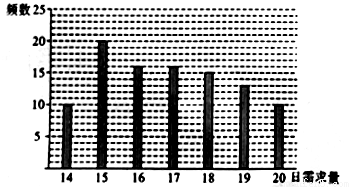
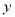 (单位:元)关于当天需求量
(单位:元)关于当天需求量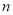 (单位:个,
(单位:个,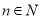 )的函数解析式;
)的函数解析式;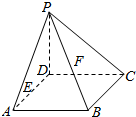 已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD
已知在四棱锥P-ABCD中,底面ABCD为菱形且∠ADC=120°,E,F分别是AD,PB的中点且PD=AD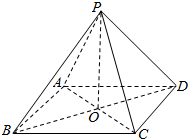 已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.
已知P是四边形ABCD所在平面外一点,PA=PB=PD,在四边形ABCD中,BA=AD,BA⊥AD,O是BD的中点,OC=$\frac{1}{2}$OA=$\frac{1}{3}$OP.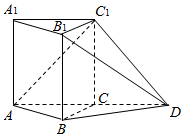 如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D
如图,在直棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=AA1=1,延长AC至D,使AC=CD,连接BD,B1D,C1D