题目内容
在(x-
)2006 的二项展开式中,含x的奇次幂的项之和为S,当x=
时,S等于 .
| 2 |
| 2 |
考点:二项式系数的性质
专题:计算题,二项式定理
分析:利用二项式定理将二项式展开,令x分别取
,-
得到两个等式,两式相减,化简即得.
| 2 |
| 2 |
解答:
解:设(x-
)2006=a0x2006+a1x2005+…+a2005x+a2006
则当x=
时,有a0(
)2006+a1(
)2005+…+a2005(
)+a2006=0(1)
当x=-
时,有a0(
)2006-a1(
)2005+…-a2005(
)+a2006=23009(2)
(1)-(2)有a1(
)2005+…+a2005(
)=-23009?
即2S=-23009
则S=-23008
故答案为:-23008.
| 2 |
则当x=
| 2 |
| 2 |
| 2 |
| 2 |
当x=-
| 2 |
| 2 |
| 2 |
| 2 |
(1)-(2)有a1(
| 2 |
| 2 |
即2S=-23009
则S=-23008
故答案为:-23008.
点评:本题考查二项式定理的展开式形式及赋值法求系数和.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
若角α的终边经过点P(-3,4),则tanα=( )
A、
| ||
B、-
| ||
C、-
| ||
D、-
|
阅读程序框图,如果输出i=5,那么在空白矩形框中填入的语句为( )


| A、S=2*i |
| B、S=2*i-1 |
| C、S=2*i-2 |
| D、S=2*i+4 |
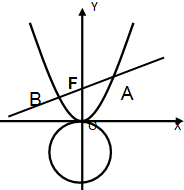 已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).
已知抛物线C:x2=4y,过焦点F的直线l与抛物线交于A,B两点(A在第一象限).