题目内容
椭圆
+
=1中,被点P(2,1)平分的弦所在直线方程是 .
| x2 |
| 9 |
| y2 |
| 4 |
考点:椭圆的简单性质
专题:圆锥曲线的定义、性质与方程
分析:若过点P的弦垂直于x轴,显然P不会是弦中点,所以可设直线斜率为k,可写出直线方程为y=kx-2k+1,带入椭圆方程可得到关于x的一元二次方程.若设该方程两根为x1,x2,根据韦达定理可求得
=2,这样即可得到关于k的方程,解方程即得k值,从而得出直线方程.
| x1+x2 |
| 2 |
解答:
解:容易判断该弦所在直线存在斜率,设为k,则直线方程为:y=kx-2k+1;
带入椭圆方程并整理得:
(4+9k2)x2+18k(1-2k)+9(1-2k)2-36=0;
根据点P是弦的中点及韦达定理得:
=2,解得k=-
;
∴所求直线方程为:y=-
x+
.
故答案为:y=-
x+
.
带入椭圆方程并整理得:
(4+9k2)x2+18k(1-2k)+9(1-2k)2-36=0;
根据点P是弦的中点及韦达定理得:
| 18k(1-2k) |
| -2(4+9k2) |
| 8 |
| 9 |
∴所求直线方程为:y=-
| 8 |
| 9 |
| 25 |
| 9 |
故答案为:y=-
| 8 |
| 9 |
| 25 |
| 9 |
点评:考查直线的点斜式方程,椭圆的标准方程,椭圆的对称性,以及韦达定理及中点坐标公式.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
函数y=2cos(
-ωx)的最小正周期是4π,则ω等于( )
| π |
| 3 |
| A、2 | ||
B、
| ||
| C、±2 | ||
D、±
|
已知a∈R,“实系数一元二次方程x2+ax+
=0的两根都是虚数”是“存在复数z同时满足|z|=2且|z+a|=1”的( )条件.
| 9 |
| 4 |
| A、充分非必要 |
| B、必要非充分 |
| C、充分必要 |
| D、既非充分又非必要 |
函数f(x)=
x+lnx的零点所在的区间是( )
| 1 |
| 2 |
| A、(0,1) |
| B、(1,2) |
| C、(2,3) |
| D、(3,4) |
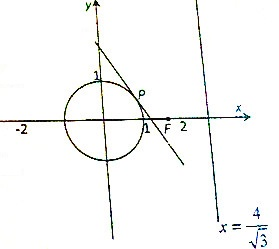 已知动点M到点F(
已知动点M到点F(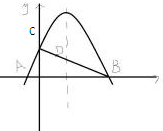 如图,抛物线y=ax2+bx+6与x轴交于AB两点与y轴交点C,已知A(-1,0)、B(3,0).
如图,抛物线y=ax2+bx+6与x轴交于AB两点与y轴交点C,已知A(-1,0)、B(3,0).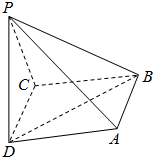 四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.
四棱锥P-ABCD的底面是边长为2的正方形,PC=2,PC⊥BC,异面直线AB与PC所成的角为60°.