题目内容
若正数x，y满足x+3y=5xy，则3x+4y的最小值是（ ）
A、
| ||
B、
| ||
| C、6 | ||
| D、5 |
考点：基本不等式
专题：不等式的解法及应用
分析：已知式子可化为
+
=1，进而可得3x+4y=（3x+4y）（
+
）
+
+
，由基本不等式可得．
| 1 |
| 5y |
| 3 |
| 5x |
| 1 |
| 5y |
| 3 |
| 5x |
| 13 |
| 5 |
| 3x |
| 5y |
| 12y |
| 5x |
解答：
解：∵正数x，y满足x+3y=5xy，
∴
=1，即
+
=1，
∴3x+4y=（3x+4y）（
+
）
=
+
+
≥
+2
=5
当且仅当
=
即x=1且y=
时取等号，
∴3x+4y的最小值为：5
故选：D
∴
| x+3y |
| 5xy |
| 1 |
| 5y |
| 3 |
| 5x |
∴3x+4y=（3x+4y）（
| 1 |
| 5y |
| 3 |
| 5x |
=
| 13 |
| 5 |
| 3x |
| 5y |
| 12y |
| 5x |
| 13 |
| 5 |
|
当且仅当
| 3x |
| 5y |
| 12y |
| 5x |
| 1 |
| 2 |
∴3x+4y的最小值为：5
故选：D
点评：本题考查基本不等式，得出
+
=1是解决问题的关键，属基础题．
| 1 |
| 5y |
| 3 |
| 5x |
练习册系列答案
津桥教育计算小状元系列答案
相关题目
如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（ ）| A、30° | B、60° |
| C、0° | D、120° |
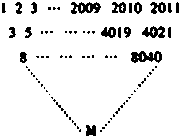给定三角形数表如图所示，其中第一行各数依次是1，2，3，…，2009，2010，2011，从第二行起，每个数分别等于它上面一行左、右两数之和，设第i行第j个数为f（i，j）（i，j∈N*，i+j≤2012），则：f（8，1）=