题目内容
过抛物线y=2x2的焦点F的直线与抛物线交于A、B两点,若|AF|=1,则|BF|=( )
A、
| ||
| B、1 | ||
C、
| ||
| D、7 |
考点:抛物线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:根据抛物线方程可求得焦点坐标和准线方程,设过F的直线方程,与抛物线方程联立,整理后,设A(x1,y1),B(x2,y2)根据韦达定理可求得x1x2的值,又根据抛物线定义可知,|AF|=y1+
,|BF|=y2+
,代入可得其值为8,再由|AF|=1,即可得到|BF|.
| 1 |
| 8 |
| 1 |
| 8 |
解答:
解:易知F坐标(0,
)准线方程为y=-
.
设过F点直线方程为y=kx+
,
代入抛物线方程,得2x2-kx-
=0.
设A(x1,y1),B(x2,y2),
则有x1x2=-
,x1+x2=
.
根据抛物线性质可知,|AF|=y1+
,|BF|=y2+
,
∴
+
=
+
=
=
=8
又由|AF|=1,则|BF|=
,
故选:A.
| 1 |
| 8 |
| 1 |
| 8 |
设过F点直线方程为y=kx+
| 1 |
| 8 |
代入抛物线方程,得2x2-kx-
| 1 |
| 8 |
设A(x1,y1),B(x2,y2),
则有x1x2=-
| 1 |
| 16 |
| k |
| 2 |
根据抛物线性质可知,|AF|=y1+
| 1 |
| 8 |
| 1 |
| 8 |
∴
| 1 |
| AF |
| 1 |
| BF |
| 1 | ||
y1+
|
| 1 | ||
y2+
|
| 2 |
| p |
| 2 | ||
|
又由|AF|=1,则|BF|=
| 1 |
| 7 |
故选:A.
点评:本题主要考查抛物线的应用和抛物线定义.对于过抛物线焦点的直线与抛物线关系,常用抛物线的定义来解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若i为虚数单位,则-i+
=( )
| 1-i |
| 1+i |
| A、-2i | ||
| B、0 | ||
C、
| ||
| D、2i |
若ω>0,且函数f(x)=4sin
cos
在[-
,
]上单调递增,则ω的取值范围是( )
| ωx |
| 2 |
| ωx |
| 2 |
| π |
| 4 |
| π |
| 3 |
A、(0,
| ||
B、(0,
| ||
| C、(0,2] | ||
| D、[2,+∞) |
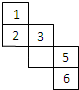 正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示.如图是一个正方体的表面展开图,若图中“4”在正方体的“前面”,则“后面”是( )
正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示.如图是一个正方体的表面展开图,若图中“4”在正方体的“前面”,则“后面”是( ) 一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点A,B所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.
一个如图所示的不规则形铁片,其缺口边界是口宽4分米,深2分米(顶点至两端点A,B所在直线的距离)的抛物线形的一部分,现要将其缺口边界裁剪为等腰梯形.