题目内容
已知二次函数f(x)=mx2+mx+2-m.
(Ⅰ)若不等式f(x)>0对任意x∈R恒成立,求实数m的取值范围;
(Ⅱ)若x=0是不等式f(x)<x唯一的整数解,求实数m的取值范围.
(Ⅰ)若不等式f(x)>0对任意x∈R恒成立,求实数m的取值范围;
(Ⅱ)若x=0是不等式f(x)<x唯一的整数解,求实数m的取值范围.
考点:二次函数的性质
专题:函数的性质及应用
分析:(Ⅰ)已知二次函数f(x)=mx2+mx+2-m,若不等式f(x)>0对任意x∈R恒成立.则:m≠0时,由
,进一步求得结果.
(Ⅱ)利用若x=0是不等式f(x)<x唯一的整数解,需要满足f(0)<0,且进一步设:令h(x)=mx2+(m-1)x+2-m,由题意得:m>2,h(0)<0,h(1)≥0,h(-1)≥0,最后求不等式组的解集.
|
(Ⅱ)利用若x=0是不等式f(x)<x唯一的整数解,需要满足f(0)<0,且进一步设:令h(x)=mx2+(m-1)x+2-m,由题意得:m>2,h(0)<0,h(1)≥0,h(-1)≥0,最后求不等式组的解集.
解答:
解:(Ⅰ)已知二次函数f(x)=mx2+mx+2-m,若不等式f(x)>0对任意x∈R恒成立.
则:m≠0时,由
解得:0<m<
(Ⅱ)由f(x)<x
得:mx2+(m-1)x+2-m<0
由f(0)<0
解得:m>2
令h(x)=mx2+(m-1)x+2-m
由题意得:m>2,h(0)<0,h(1)≥0,h(-1)≥0
解得:2<m≤3
则:m≠0时,由
|
解得:0<m<
| 8 |
| 5 |
(Ⅱ)由f(x)<x
得:mx2+(m-1)x+2-m<0
由f(0)<0
解得:m>2
令h(x)=mx2+(m-1)x+2-m
由题意得:m>2,h(0)<0,h(1)≥0,h(-1)≥0
解得:2<m≤3
点评:本题考查的知识要点:二次函数恒大于0的条件,及一元二次不等式有某一个唯一实数解的条件,及相关的不等式的解法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
若函数f(x)的导数为-2x2+1,则f(x)可以等于( )
| A、-2x3+1 | ||
B、-
| ||
| C、x+1 | ||
| D、-4x |
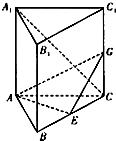 如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.
如图,在直三棱柱ABC-A1B1C1中,∠BAC=90°,AC=AB=AA1,E是BC的中点.