题目内容
1.在△ABC中,D为线段BC上一点,且$BD=\frac{1}{5}BC$,以向量$\overrightarrow{AB},\overrightarrow{AC}$作为一组基底,则$\overrightarrow{AD}$等于( )| A. | $\frac{1}{5}\overrightarrow{AB}+\frac{4}{5}\overrightarrow{AC}$ | B. | $\frac{2}{5}\overrightarrow{AB}+\frac{3}{5}\overrightarrow{AC}$ | C. | $\frac{3}{5}\overrightarrow{AB}+\frac{2}{5}\overrightarrow{AC}$ | D. | $\frac{4}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$ |
分析 由题意作图辅助,从而可得$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$=$\overrightarrow{AB}$+$\frac{1}{5}$($\overrightarrow{AC}$-$\overrightarrow{AB}$),从而化简即可.
解答 解:由题意作图如右,
$\overrightarrow{AD}$=$\overrightarrow{AB}$+$\overrightarrow{BD}$
=$\overrightarrow{AB}$+$\frac{1}{5}$$\overrightarrow{BC}$
=$\overrightarrow{AB}$+$\frac{1}{5}$($\overrightarrow{AC}$-$\overrightarrow{AB}$)
=$\frac{4}{5}\overrightarrow{AB}+\frac{1}{5}\overrightarrow{AC}$,
故选:D.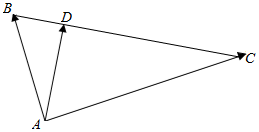
点评 本题考查了平面向量的线性运算的应用及数形结合的思想应用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
12.设x∈R,则“1-x-2x2<0”是“|2-x|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
9.已知复数z满足(1+i)z=(1-i)2,则z的共轭复数的虚部为( )
| A. | 2 | B. | -2 | C. | -1 | D. | 1 |
16.已知直线l1:A1x+B1y+1=0,直线l2:A2x+B2y+1=0,A1,A2,B1,B2∈R,则“l1⊥l2”的充分且必要条件是( )
| A. | A1A2-B1B2=0 | B. | A1A2+B1B2=0 | C. | A1B2-A2B1=0 | D. | A1B2+A2B1=0 |