题目内容
奇函数f（x）在[3，6]上是增函数，在区间[3，6]上的最大值为8，最小值为-1，则2f（-6）+f（-3）= ．
考点：奇偶性与单调性的综合
专题：函数的性质及应用
分析：先利用条件找到f（3）=-1，f（6）=8，再利用f（x）是奇函数求出f（-3），f（-6）代入即可．
解答：
解：由题意f（x）在区间[3，6]上是增函数，在区间[3，6]上的最大值为8，最小值为-1，
得f（3）=-1，f（6）=8，
∵f（x）是奇函数，
∴f（-3）+2f（-6）=-f（3）-2f（6）=1-2×8=-15．
故答案为：-15．
得f（3）=-1，f（6）=8，
∵f（x）是奇函数，
∴f（-3）+2f（-6）=-f（3）-2f（6）=1-2×8=-15．
故答案为：-15．
点评：本题考查了函数奇偶性和单调性的应用．若已知一个函数为奇函数，则应有其定义域关于原点对称，且对定义域内的一切x都有f（-x）=-f（x）成立，本题属于基础题．
练习册系列答案
相关题目
过抛物线y2=10x的焦点作一条直线与抛物线相交于A、B两点，它们的横坐标之和等于5，则这样的直线（ ）
| A、有且仅有一条 |
| B、有且仅有两条 |
| C、有无穷多条 |
| D、不存在 |
若x、y满足约束条件
目标函数z=ax+2y仅在点（1，0）处取得最小值，则a的取值范围是（ ）
|
| A、（-4，2） |
| B、（-1，2） |
| C、（-4，0） |
| D、（-2，4） |
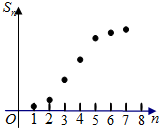某工厂前n年的总产量Sn与n之间的关系如图所示．从目前记录的结果看，前m年的年平均产量最高．m值为（ ）| A、2 | B、4 | C、5 | D、8 |
设函数f（x）的零点为x1，g（x）=4x+2x-2的零点为x2，若|x1-x2|≤0.25，则f（x）可以是（ ）
| A、f（x）=（x-1）2 | ||
| B、f（x）=ex-1 | ||
C、f(x)=ln(x-
| ||
| D、f（x）=4x-1 |