题目内容
函数y=x2-2x-3，x∈[-1，2）的值域（ ）
| A、（-3，0] |
| B、[-4，0） |
| C、[-4，0] |
| D、[-3，0） |
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：由二次函数的性质可得函数的对称轴，与开口方向，然后求解可得．
解答：
解：可得函数y=x2-2x-3的图象为开口向上的抛物线，
对称轴为x=1，
故当x=1时，y取最小值-4，
当x=-1时，y取最大值0，
故所求函数的值域为[-4，0]．
故选：C．
对称轴为x=1，
故当x=1时，y取最小值-4，
当x=-1时，y取最大值0，
故所求函数的值域为[-4，0]．
故选：C．
点评：本题考查二次函数区间的最值，得出函数的单调性是解决问题的关键，属基础题．
练习册系列答案
阅读快车系列答案
相关题目
函数y=x2+2x-4的定义域是（-2，5]，则其值域是（ ）
| A、（4，31] |
| B、[-5，-4] |
| C、（-5，31] |
| D、[-5，31] |
一个四棱锥的三视图如图所示，其侧视图是等边三角形，该四棱锥的体积等于（ ）
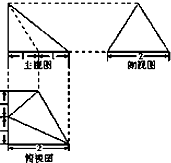
A、
| ||
B、2
| ||
C、3
| ||
D、6
|