题目内容
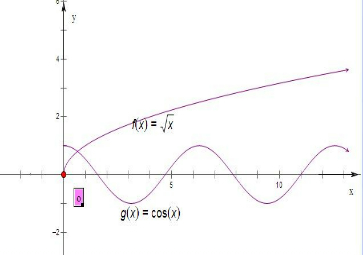
(文做)函数f(x)=
的图象与g(x)=cosx的图象在[0,+∞)内( )
| x |
| A、没有交点 |
| B、有且仅有一个交点 |
| C、尤其仅有两个交点 |
| D、有无穷多个交点 |
考点:余弦函数的图象
专题:函数的性质及应用,三角函数的图像与性质
分析:通过讨论在x∈[0,
]内,有且仅有一个交点,当x∈[
,+∞)时,
≥
>1,-1≤cosx≤1,可得H(x)>0无零点,得解.
| π |
| 2 |
| π |
| 2 |
| x |
|
解答:
 解:令H(x)=
解:令H(x)=
-cosx,则在x∈[0,
]内,
当x=0时,有H(x)=0-1=-1<0;
当x=
时,有H(x)=
-0=
>0;
且在x∈[0,
]内,f(x)=
,是单调递增的,g(x)=cosx是单调递减的,
故x∈[0,
]内有且仅有一个交点.
当x∈[
,+∞)时,
≥
>1,-1≤cosx≤1,
∴H(x)>0,无零点,
综上可知,函数f(x)=
的图象与g(x)=cosx的图象在[0,+∞)内,有且仅有一个交点.
故选:B.
 解:令H(x)=
解:令H(x)=| x |
| π |
| 2 |
当x=0时,有H(x)=0-1=-1<0;
当x=
| π |
| 2 |
|
|
且在x∈[0,
| π |
| 2 |
| x |
故x∈[0,
| π |
| 2 |
当x∈[
| π |
| 2 |
| x |
|
∴H(x)>0,无零点,
综上可知,函数f(x)=
| x |
故选:B.
点评:本题主要考查了函数的性质及应用,三角函数的图象与性质,属于基本知识的考查.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 已知抛物线C1:x2=4py,圆C2:x2+(y-p)2=p2,直线l:y=
已知抛物线C1:x2=4py,圆C2:x2+(y-p)2=p2,直线l:y=| 1 |
| 2 |
| AB |
| CD |
A、
| ||
B、
| ||
C、
| ||
| D、p2 |
下列有关命题的说法正确的是( )
| A、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” |
| B、“x=-1”是“x2-5x-6=0”的必要不充分条件 |
| C、命题“若x=y,则sinx=siny”的逆否命题为真命题 |
| D、若命题p:“?x0∈R使x02+x0+1<0”,则¬p为假命题 |
 如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=
如图,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径作圆与斜边AB交于点D,则BD的长为=