题目内容
下面一组图形为三棱锥P-ABC的底面与三个侧面.已知AB⊥BC,PA⊥AB,PA⊥AC.

(1)在三棱锥P-ABC中,求证:平面ABC⊥平面PAB;
(2)在三棱锥P-ABC中,M是PA的中点,且PA=BC=3,AB=4,求三棱锥P-MBC的体积.

(1)在三棱锥P-ABC中,求证:平面ABC⊥平面PAB;
(2)在三棱锥P-ABC中,M是PA的中点,且PA=BC=3,AB=4,求三棱锥P-MBC的体积.
考点:棱柱、棱锥、棱台的体积,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(1)根据三视图得出空间几何体,运用判定定理证明,
(2)运用体积公式求解即可VP-MBC=VP-ABC-VM-ABC.
(2)运用体积公式求解即可VP-MBC=VP-ABC-VM-ABC.
解答:
 证明:(1)如图,证明:∵PA⊥AB,PA⊥AC,
证明:(1)如图,证明:∵PA⊥AB,PA⊥AC,
AB∩AC=A,∴PA⊥平面ABC,又∵PA?平面ABP
∴平面ABC⊥平面PAB
解:(2)∵PA=3,M是PA的中点,∴MA=
.
又∵AB=4,BC=3.
∴VM-ABC=
S△ABC•MA=
×
×4×3×
=3
又VP-ABC=
S△ABC•PA=
×
×4×3×3=6,
∴VP-MBC=VP-ABC-VM-ABC=6-3=3
 证明:(1)如图,证明:∵PA⊥AB,PA⊥AC,
证明:(1)如图,证明:∵PA⊥AB,PA⊥AC,AB∩AC=A,∴PA⊥平面ABC,又∵PA?平面ABP
∴平面ABC⊥平面PAB
解:(2)∵PA=3,M是PA的中点,∴MA=
| 3 |
| 2 |
又∵AB=4,BC=3.
∴VM-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
又VP-ABC=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
∴VP-MBC=VP-ABC-VM-ABC=6-3=3
点评:本题考查了空间几何体的三视图的运用,判断面面垂直问题,秋季体积,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
(文做)函数f(x)=
的图象与g(x)=cosx的图象在[0,+∞)内( )
| x |
| A、没有交点 |
| B、有且仅有一个交点 |
| C、尤其仅有两个交点 |
| D、有无穷多个交点 |
(文数)已知函数y=tanwx在(-
,
)内是增函数,则( )
| π |
| 2 |
| π |
| 2 |
| A、0<w≤1 | B、-1≤w<0 |
| C、w≥1 | D、w≤-1 |
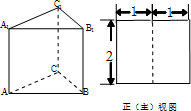 如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )
如图,三棱柱ABC-A1B1C1的侧棱长和底面边长均为2,且侧棱AA1⊥底面ABC,其正(主)视图是边长为2的正方形,则此三棱柱侧(左)视图的面积为( )