题目内容
已知x1,x2是函数f(x)=e-x-|lnx|的两个零点,则( )
A.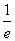 <x1x2<1 B.1<x1x2<e
<x1x2<1 B.1<x1x2<e
C.1<x1x2<10 D.e<x1x2<10
A
[解析] 在同一坐标系中画出函数y=e-x与y=|lnx|的图象(图略),结合图象不难看出,在x1,x2中,其中一个属于区间(0,1),另一个属于区间(1,+∞).不妨设x1∈(0,1),x2∈(1,+∞),则有e-x1=|lnx1|=-lnx1∈(e-1,1),e-x2=|lnx2|=lnx2∈(0,e-1),e-x2-e-x1=lnx2+lnx1=ln(x1x2)∈(-1,0).于是有e-1<x1x2<e0,即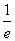 <x1x2<1,选A.
<x1x2<1,选A.

练习册系列答案
相关题目
 越大,线性相关程度越大
越大,线性相关程度越大 且
且
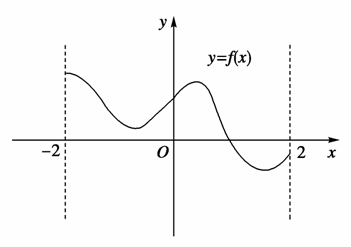
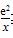 (x>0).
(x>0).
 D.2
D.2 ,则函数
,则函数 的最小正周期是 。
的最小正周期是 。