题目内容
函数f(x)＝xex－a有两个零点，则实数a的取值范围是________．
(－
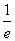，0)
[解析] 令f ′(x)＝(x＋1)ex＝0，得x＝－1，则当x∈(－∞，－1)时，f ′(x)<0，当x∈(－1，＋∞)时，f ′(x)>0，f(x)在(－∞，－1)上单调递减，在(－1，＋∞)上单调递增，要使f(x)有两个零点，则极小值f(－1)<0，即－e－1－a<0，∴a>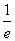－，又x→－∞时，f(x)>0，则a<0，∴a∈(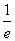－，0)．
练习册系列答案
相关题目
B．－
的定义域是非零实数，且在(－∞，0)上是增函数，在(0，＋∞)上是减函数，则最小的自然数a＝________.
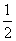D.