题目内容
6.已知函数$f(x)=\left\{\begin{array}{l}-sinx,x>0\\ sinx,x≤0\end{array}\right.$,则下列结论正确的是( )| A. | f(x)是奇函数 | |
| B. | f(x)是偶函数 | |
| C. | f(x)是周期函数 | |
| D. | f(x)在$[-\frac{π}{2}+2kπ,\frac{π}{2}+2kπ](k∈z)$上为减函数 |
分析 利用偶函数的定义,即可得出结论.
解答 解:由题意,x>0,则-x<0,f(-x)=sin(-x)=-sinx=f(x),
同理,x<0,f(-x)=f(x),∴函数f(x)是偶函数.
故选B.
点评 本题考查偶函数的定义,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
16.在直三棱柱ABC-A1BlC1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
17.设抛物线x2=4y的焦点为F,过点F作斜率为k(k>0)的直线l与抛物线相交于A、B两点,且点P恰为AB的中点,过点P作x轴的垂线与抛物线交于点M,若|MF|=4,则直线l的方程为( )
| A. | $y=2\sqrt{2}x+1$ | B. | $y=\sqrt{3}x+1$ | C. | $y=\sqrt{2}x+1$ | D. | $y=2\sqrt{3}x+2$ |
14.某几何体的三视图如图所示,其俯视图是由一个半圆与其直径组成的图形,则此几何体的体积是( )
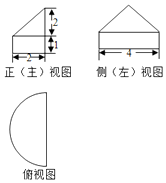

| A. | 3π | B. | $\frac{10π}{3}$ | C. | $\frac{11π}{3}$ | D. | 4π |
1.已知函数f(x)满足条件:?x∈R,f(x)+f(-x)=0且f(x+t)-f(x)<0(其中t为正数),则函数f(x)的解析式可以是( )
| A. | y=xsinx+3 | B. | y=x3 | C. | y=-sinx | D. | y=-3x |
16.如图所示的程序框图中,输出的S的值是( )
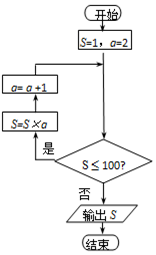

| A. | 80 | B. | 100 | C. | 120 | D. | 140 |
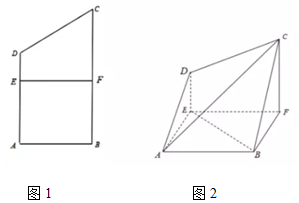 已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.
已知四边形ABCD为直角梯形,AD∥BC,AB⊥BC,BC=2AB=4,AD=3,F为BC中点,EF∥AB,EF与AD交于点E,沿EF将四边形EFCD折起,使得平面ABFE⊥平面EFCD,连接AD,BC,AC.