题目内容
17.已知函数f(x)=log2x,若数列{an}的各项使得2,f(a1),f(a2),…,f(an),2n+4成等差数列,则数列{an}的前n项和)| A. | $\frac{4}{3}$(4n-1) | B. | $\frac{16}{3}$(4n-1) | C. | $\frac{16}{3}$(2n-1) | D. | $\frac{4}{3}$(2n-1) |
分析 可求得d=$\frac{2n+4-2}{n+2-1}$=2,从而解得f(an)=2n+2,从而求得an=22n+2=4n+1,从而求和.
解答 解:∵2,f(a1),f(a2),…,f(an),2n+4成等差数列,
∴d=$\frac{2n+4-2}{n+2-1}$=2,
∴f(an)=2+(n+1-1)2=2n+2,
即log2an=2n+2,
故an=22n+2=4n+1,
故数列{an}是以16为首项,4为公比的等比数列;
故Sn=$\frac{16(1-{4}^{n})}{1-4}$=$\frac{16}{3}$(4n-1),
故选:B.
点评 本题考查了等差数列与等比数列的应用.

练习册系列答案
 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案
相关题目
7.设全集为R,集合A={y|y>2},B={x|-1≤x≤4},则(∁RA)∩B=( )
| A. | (2,4] | B. | [-1,2] | C. | [-1,4] | D. | (4,+∞) |
12.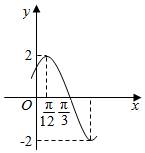 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
 已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,下列说法正确的是( )| A. | ω=2,φ=$\frac{π}{6}$ | |
| B. | f(x)的图象关于点(-$\frac{5π}{12}$,0)对称 | |
| C. | 若方程f(x)=m在[-$\frac{π}{2}$,0]上有两个不相等的实数根,则实数m的取值范围是(-2,-$\sqrt{3}$] | |
| D. | 将函数y=2cos(2x+$\frac{π}{3}$)的图象向右平移$\frac{π}{12}$的单位得到函数f(x)的图象 |
9.输人N的值为5,按如图所示的程序框图运行后,输出的结果是( )


| A. | $\frac{24}{25}$ | B. | $\frac{35}{36}$ | C. | $\frac{48}{49}$ | D. | $\frac{63}{64}$ |