题目内容
5.已知椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),A、B为椭圆的左右顶点,抛物线C2:y=-x2+1的顶点恰是椭圆的一个焦点,且点A、B在抛物线上.(1)求椭圆的方程;
(2)过点B的直线l与C1在x轴的上方交于P点,与C2在x轴的下方交于Q点,若AP⊥AQ,求直线l的方程.
分析 (1)由已知焦点F(0,1),从而c=1,由点A、B在抛物线上,得-b2+1=0,由此能求出椭圆的方程.
(2)设直线l方程为y=k(x-1)(k≠0),代入C1的方程,得(k2+2)x2-2k2x+k2-2=0,点P(xp,yp),推导出点P的坐标为($\frac{{k}^{2}-2}{{k}^{2}+2},\frac{-4k}{{k}^{2}+2}$).由$\left\{\begin{array}{l}{y=k(x-1),k≠0}\\{y=-{x}^{2}+1}\end{array}\right.$,得点Q的坐标为(-k-1,-k2-2k),由AP⊥AQ,能求出k,从而能求出直线l的方程.
解答 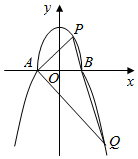 解:(1)∵椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),A、B为椭圆的左右顶点
解:(1)∵椭圆C1:$\frac{{y}^{2}}{{a}^{2}}$+$\frac{{x}^{2}}{{b}^{2}}$=1(a>b>0),A、B为椭圆的左右顶点
抛物线C2:y=-x2+1的顶点恰是椭圆的一个焦点,
∴焦点F(0,1),∴c=1,
∵点A、B在抛物线上,∴-b2+1=0,∴b=1,
∴a2=1+1=2,
∴椭圆的方程为$\frac{{y}^{2}}{2}+{x}^{2}$=1.
(2)∵椭圆的方程为$\frac{{y}^{2}}{2}+{x}^{2}$=1,直线l与x轴不重合也不垂直,设其方程为y=k(x-1)(k≠0),
代入C1的方程,整理得
(k2+2)x2-2k2x+k2-2=0.(*)
设点P(xp,yp),
∵直线l过点B(1,0),
∴x=1是方程(*)的一个根,
由求根公式,得xp=$\frac{{k}^{2}-2}{{k}^{2}+2}$,从而yp=$\frac{-4k}{{k}^{2}+2}$,
∴点P的坐标为($\frac{{k}^{2}-2}{{k}^{2}+2},\frac{-4k}{{k}^{2}+2}$).
同理,由$\left\{\begin{array}{l}{y=k(x-1),k≠0}\\{y=-{x}^{2}+1}\end{array}\right.$,得点Q的坐标为(-k-1,-k2-2k),
∴$\overrightarrow{AP}$=($\frac{2{k}^{2}}{{k}^{2}+2}$,$\frac{-4k}{{k}^{2}+2}$),$\overrightarrow{AQ}$=(-k,-k2-2k),
∵AP⊥AQ,∴$\overrightarrow{AP}•\overrightarrow{AQ}$=0,
即$\frac{2{k}^{2}}{{k}^{2}+2}•(-k)+\frac{-4k}{{k}^{2}+2}•(-{k}^{2}-2k)$=0,
∵k≠0,∴-k+2(k+2)=0,解得k=-4.
∴直线l的方程为y=-4(x-1).
点评 本题考查椭圆方程的求法,考查直线方程的求法,是中档题,解题时要认真审题,注意椭圆性质、韦达定理、向量的数量积等知识点的合理运用.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{5π}{6}$ |
| A. | 1 | B. | -1 | C. | -i | D. | i |
| A. | $\frac{4}{3}$(4n-1) | B. | $\frac{16}{3}$(4n-1) | C. | $\frac{16}{3}$(2n-1) | D. | $\frac{4}{3}$(2n-1) |
| A. | f(m+1)≥0 | B. | f(m+1)≤0 | C. | f(m+1)>0 | D. | f(m+1)<0 |
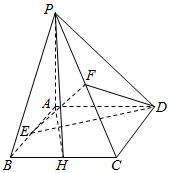 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点