题目内容
2.设复数z1,z2在复平面内的对应点关于虚轴对称,z1=1+2i,i为虚数单位,则z1z2=-5.分析 利用复数的运算法则与共轭复数的定义、几何意义即可得出.
解答 解:∵复数z1、z2在复平面内的对应点关于虚轴对称,z1=1+2i,
∴z2=-1+2i.
∴z1•z2=(1+2i)(-1+2i)=-5.
故答案为:-5.
点评 本题考查了复数的运算法则与共轭复数的定义、几何意义,属于基础题.

练习册系列答案
 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案 互动课堂系列答案
互动课堂系列答案
相关题目
10.已知$\frac{(1-i)^{2}}{z}$=1+i(i为虚数单位),则复数z的虚部为( )
| A. | 1 | B. | -1 | C. | -i | D. | i |
17.已知函数f(x)=log2x,若数列{an}的各项使得2,f(a1),f(a2),…,f(an),2n+4成等差数列,则数列{an}的前n项和)
| A. | $\frac{4}{3}$(4n-1) | B. | $\frac{16}{3}$(4n-1) | C. | $\frac{16}{3}$(2n-1) | D. | $\frac{4}{3}$(2n-1) |
14.设函数f(x)=x2+x+a(a>0),且f(m)<0,则( )
| A. | f(m+1)≥0 | B. | f(m+1)≤0 | C. | f(m+1)>0 | D. | f(m+1)<0 |
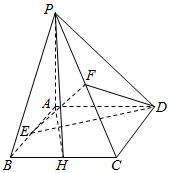 如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点
如图,四棱锥P-ABCD的底面为正方形,侧面PAD⊥底面ABCD,PA⊥AD,E,F,H分别为AB,PC,BC的中点