题目内容
在一个盒子中装有6枝圆珠笔,其中3枝黑色,2枝蓝色,1枝红色,从中任取3枝.
(1)该实验的基本事件共有多少个?若将3枝黑色圆珠笔编号为A、B、C,2枝蓝色圆珠笔编号为d,e,1枝红色圆珠笔编号为x,用{a,b,c}表示基本事件,试列举出该实验的所有基本事件;
(2)求恰有一枝黑色的概率;
(3)求至少1枝蓝色的概率.
(1)该实验的基本事件共有多少个?若将3枝黑色圆珠笔编号为A、B、C,2枝蓝色圆珠笔编号为d,e,1枝红色圆珠笔编号为x,用{a,b,c}表示基本事件,试列举出该实验的所有基本事件;
(2)求恰有一枝黑色的概率;
(3)求至少1枝蓝色的概率.
考点:互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)所有情况一一列举出来即可,
(2)恰有一枝黑色的概率,找到满足条件的基本事件,根据概率公式计算即可,
(3)求出没有蓝色的取法,根据互斥事件的概率公式计算即可.
(2)恰有一枝黑色的概率,找到满足条件的基本事件,根据概率公式计算即可,
(3)求出没有蓝色的取法,根据互斥事件的概率公式计算即可.
解答:
解:(1)3枝黑色圆珠笔编号为A、B、C,2枝蓝色圆珠笔编号为d,e,1枝红色圆珠笔编号为x则从中任取3枝的总的取法为:
(A、B、C),(A、B、d),(A、B、e),(A、B、x),(A、C、d),
(A、C、e),(A、C、x),(B、C、d),(B、C、e),(B、C、x),(A、d、e),(A、d、x),
(A、e、x),(B、d、e),(B、d、x),(B、e、x),(C、d、e),(C、d、x),(C、e、x),
(d、e、x)共20种,
(1)其中恰有一枝黑色的取法有(A、B、d),(A、B、e),(A、B、x),(A、C、d),
(A、C、e),(A、C、x),(B、C、d),(B、C、e),(B、C、x)共9种,
故恰有一枝黑色的概率P=
,A,B,C)
(2)没有蓝色的取法有(A,B,C)(A,B,X),(B,C,x),(A,C,X),
故至少1枝蓝色的概率为P=1-
=
(A、B、C),(A、B、d),(A、B、e),(A、B、x),(A、C、d),
(A、C、e),(A、C、x),(B、C、d),(B、C、e),(B、C、x),(A、d、e),(A、d、x),
(A、e、x),(B、d、e),(B、d、x),(B、e、x),(C、d、e),(C、d、x),(C、e、x),
(d、e、x)共20种,
(1)其中恰有一枝黑色的取法有(A、B、d),(A、B、e),(A、B、x),(A、C、d),
(A、C、e),(A、C、x),(B、C、d),(B、C、e),(B、C、x)共9种,
故恰有一枝黑色的概率P=
| 9 |
| 20 |
(2)没有蓝色的取法有(A,B,C)(A,B,X),(B,C,x),(A,C,X),
故至少1枝蓝色的概率为P=1-
| 4 |
| 20 |
| 4 |
| 5 |
点评:本题考查了等可能事件的概率,如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
,此题属中档题.
| m |
| n |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知函数f(x)=
x2-ax+lnx在(0,+∞)上是增函数,则a的取值范围是( )
| 1 |
| 2 |
| A、(-∞,2) |
| B、(-∞,2] |
| C、(-2,2) |
| D、[-2,2] |
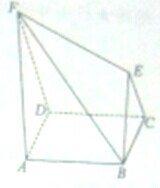 在如图所示的几何体中,四边形ABCD为正方形,DF∥CE,DF⊥DC,且DF=2AD=2CE,AF=
在如图所示的几何体中,四边形ABCD为正方形,DF∥CE,DF⊥DC,且DF=2AD=2CE,AF=