题目内容
对任意复数z=x+yi（x，y∈R），i为虚数单位，则下列结论正确的是（ ）
| A、|z|≤|x|+|y| | ||
B、|z-
| ||
| C、z2=x2+y2 | ||
D、|z-
|
考点：复数求模
专题：数系的扩充和复数
分析：利用复数模的概念，结合基本不等式判断即可．
解答：
解：∵z=x+yi（x，y∈R），
∴|z|2=x2+y2≤x2+y2+2|x||y|=（|x|+|y|）2，
∴|z|≤|x|+|y|，即A正确，C错误；
又|z-
|=2|y|，可排除B与D，
故选：A．
∴|z|2=x2+y2≤x2+y2+2|x||y|=（|x|+|y|）2，
∴|z|≤|x|+|y|，即A正确，C错误；
又|z-
. |
| z |
故选：A．
点评：本题考查复数求模，考查复数的概念的应用，属于基础题．
练习册系列答案
相关题目
某算法的程序框图如图所示，则输出的S的值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
若
=42，则
的值为（ ）
| C | 2 n |
| A | 2 2 |
| C | 3 n |
| A、6 | B、7 | C、35 | D、20 |
为了得到函数y=sin（3x+1），x∈R的图象，只需将函数y=sin3x，x∈R的图象（ ）
| A、向左平移1个的单位长度 | ||
| B、向右平移1个的单位长度 | ||
C、向左平移
| ||
D、向右平移
|
将一个骰子抛掷一次，设事件A表示向上的一面出现的点数不超过3，事件B表示向上的一面出现的点数不小于4，事件C表示向上的一面出现奇数点，则（ ）
| A、A与B是互斥而非对立事件 |
| B、A与B是对立事件 |
| C、B与C是互斥而非对立事件 |
| D、B与C是对立事件 |
在1万km2的海域中有40km2的大陆架贮藏着石油，假如在海域中任意一点钻探，钻到油层面的概率是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
已知函数f(x)=
x2-ax+lnx在（0，+∞）上是增函数，则a的取值范围是（ ）
| 1 |
| 2 |
| A、（-∞，2） |
| B、（-∞，2] |
| C、（-2，2） |
| D、[-2，2] |
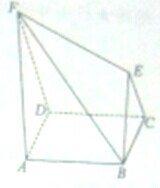在如图所示的几何体中，四边形ABCD为正方形，DF∥CE，DF⊥DC，且DF=2AD=2CE，AF=