题目内容
若函数f(x)=x2+mx+n,对任意实数x都有f(2-x)=f(2+x)成立,试比较f(-1),f(2),f(4)的大小.
考点:二次函数的性质
专题:函数的性质及应用
分析:根据f(2-x)=f(2+x)知f(x)的对称轴x=2,根据-1,2,4这三个数和对称轴的距离,结合二次函数图象即可比较出f(-1),f(2),f(4)的大小关系.
解答:
解:由已知条件知,f(x)的对称轴为x=2;
根据-1,2,4这几个数到对称轴的距离,即可比较对应函数值的大小;
即到对称轴的距离越大函数值越大;
2-(-1)=3,2-2=0,4-2=2;
∴f(-1)>f(4)>f(2).
根据-1,2,4这几个数到对称轴的距离,即可比较对应函数值的大小;
即到对称轴的距离越大函数值越大;
2-(-1)=3,2-2=0,4-2=2;
∴f(-1)>f(4)>f(2).
点评:考查二次函数的对称轴,二次函数图象开口向上时,数轴上的点和对称轴的距离越大,对应函数值越大.

练习册系列答案
相关题目
执行如图所示的程序框图,若f(x)=3x2-1,取?=
,则输出的值为( )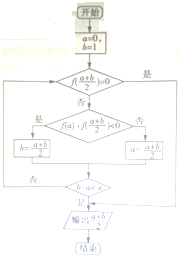
| 1 |
| 10 |

A、
| ||
B、
| ||
C、
| ||
D、
|
若0<m<1,0<n<1,则
的最大值为( )
| mn(1-m-n) |
| (m+n)(1-m)(1-n) |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
函数y=ln
的图象大致为( )
| 1 |
| |2x-3| |
A、 |
B、 |
C、 |
D、 |
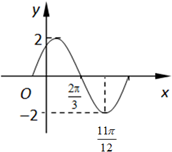 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)在一个周期内的图象如图所示.