Question

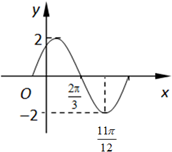已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）在一个周期内的图象如图所示．
（1）求函数f（x）的解析式；
（2）求函数f（x）在[-

π

6

，

π

4

]的最大值和最小值．

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式,三角函数的最值

专题：三角函数的求值

分析：（1）求出函数的振幅，周期，得到角频率，利用函数经过的特殊点求出初相，即可求出函数的解析式．
（2）利用x的范围求出相位的范围，通过三角函数的值域求解函数的值域即可．

解答： 解：（1）由图可知A=2，…（1分）

T

4

=

11π

12

-

2π

3

=

π

4

，∴T=π．
∴ω=

2π

π

=2…（3分）
∴f（x）=2sin（2x+φ）．
又因为函数图象过点(

11π

12

，-2)，
∴2sin(

11π

6

+φ)=-2，
∴

11π

6

+φ=

3π

2

+2kπ，k∈Z，
∴φ=2kπ-

π

3

，k∈Z…（5分）
又∵|π|＜π∴φ=-

π

3

∴f(x)=2sin(2x-

π

3

)．…（7分）
（2）令2x-

π

3

=t∵x∈[-

π

6

，

π

4

]∴t∈[-

2π

3

，

π

6

]，…（9分）
∴sint∈[-1，

1

2

]，…（12分）
∴f（x）的值域为[-2，1]．…（14分）

点评：本题考查函数的解析式的求法，三角函数的值域的求法，考查计算能力．