题目内容
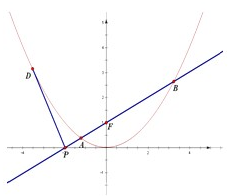 抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.
抛物线C:x2=4y,直线AB过抛物线C的焦点F,交x轴于点P.(Ⅰ)求证:PF2=PA•PB;
(Ⅱ)过P作抛物线C的切线,切点为D(异于原点),
(1)kDA•kDF•kDB是否恒成等差数列,请说明理由;
(2)△ABD重心的轨迹是什么图形,请说明理由.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由于F点的坐标已知,设出AB方程,求出P点坐标,联立直线与抛物线方程,得到一个关于x的一元二次方程,利用韦达定理能证明PF2=PA•PB.
(Ⅱ)(i)根据题意分别求出kDA,kDF,kDB,结合韦达定理验证2kDF=kDA+kDB是否成立.
(i)由三角形重心坐标公式,结合韦达定理消去参数k,即得到重心的轨迹.
(Ⅱ)(i)根据题意分别求出kDA,kDF,kDB,结合韦达定理验证2kDF=kDA+kDB是否成立.
(i)由三角形重心坐标公式,结合韦达定理消去参数k,即得到重心的轨迹.
解答:
(Ⅰ)证明:∵ 抛物线C:x2=4y的焦点F(0,1),
抛物线C:x2=4y的焦点F(0,1),
∴设直线AB为:y=kx+1,
联立
,得x2-4kx-4=0,
设P(x0,0),A(x1,y1),F(0,1),B(x2,y2),
x1+x2=4k,x1x2=-4,
y1y2=(kx1+1)(kx2+1)
=k2x1x1=+k(x1+x2)+1
=-4k2+4k2+1=1.
∵
=(-x0,1),
=(x1-x0,y1),
=(x2-x0,y2),
又x0=-
,
2=
+1,
•
=(x1+
)(x2+
)+y1y2
=x1x2+
(x1+x2)+
+1
=
+1.
∴
2=
•
.
∴PF2=PA•PB.
(Ⅱ)(i)设D(x,
),y=
的导数为y′=
,
∴
=
,解得x=-
,∴D(-
,
),
2kDF=2(
-
)=k-
,
kDA+kDB=
=
=
=
=k-
.
∴2kDF=kDA+kDB,
∴kDA•kDF•kDB恒成等差数列.
(ii)∵△ABD重心坐标(x,y),由题意得(-
+x1+x2,
+y1+y2),
即(-
+4k,
+4k2+2),
由
,消去k,得x2=
(y-2),
∴△ABD重心的轨迹是抛物线x2=
(y-2).
 抛物线C:x2=4y的焦点F(0,1),
抛物线C:x2=4y的焦点F(0,1),∴设直线AB为:y=kx+1,
联立
|
设P(x0,0),A(x1,y1),F(0,1),B(x2,y2),
x1+x2=4k,x1x2=-4,
y1y2=(kx1+1)(kx2+1)
=k2x1x1=+k(x1+x2)+1
=-4k2+4k2+1=1.
∵
| PF |
| PA |
| PB |
又x0=-
| 1 |
| k |
| PF |
| 1 |
| k2 |
| PA |
| PB |
| 1 |
| k |
| 1 |
| k |
=x1x2+
| 1 |
| k |
| 1 |
| k2 |
=
| 1 |
| k2 |
∴
| PF |
| PA |
| PB |
∴PF2=PA•PB.
(Ⅱ)(i)设D(x,
| x |
| 4 |
| x2 |
| 4 |
| x |
| 2 |
∴
| ||
x+
|
| x |
| 2 |
| 2 |
| k |
| 2 |
| k |
| 1 |
| k2 |
2kDF=2(
| k |
| 2 |
| 1 |
| 2k |
| 1 |
| k |
kDA+kDB=
kx1+1-
| ||
x1+
|
kx2+1-
| ||
x2+
|
=
| 2k5x1x2+(3k4-k2)(x1+x2)+4k(k2-1) |
| k2[k2x1x2+2k(x1+x2)+4] |
=
| 4k(k4-1) |
| 4k2(k2+1) |
=k-
| 1 |
| k |
∴2kDF=kDA+kDB,
∴kDA•kDF•kDB恒成等差数列.
(ii)∵△ABD重心坐标(x,y),由题意得(-
| 2 |
| k |
| 1 |
| k2 |
即(-
| 2 |
| k |
| 1 |
| k2 |
由
|
| 4 |
| 3 |
∴△ABD重心的轨迹是抛物线x2=
| 4 |
| 3 |
点评:本题考查PF2=PA•PB的证明,考查等差数列的判断,考查三角形重心的轨迹的求法,解题时要认真审题,注意意三角形重心坐标公式的合理运用.

练习册系列答案
相关题目
图示是由几个相同的小正方体搭成的一个几何体,它的俯视图是( )


A、 |
B、 |
C、 |
D、 |
已知函数f(x)是奇函数,且当x>0时,f(x)=x2+
,则f(-1)=( )
| 1 |
| x |
| A、-2 | B、0 | C、1 | D、2 |
已知数列{an}满足a1=1,an+1=
an,n∈N*,其前n项和为Sn,则( )
| 2 |
| 3 |
| A、Sn=2an-1 |
| B、Sn=3an-2 |
| C、Sn=4-3an |
| D、Sn=3-2an |
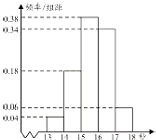 高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.
高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图.