题目内容
10．数列{an}中${a_1}=\frac{1}{2}，{a_{n+1}}=\frac{a_n}{{1+3{a_n}}}$，记数列$\{\frac{1}{a_n}\}$的前n项和为Tn，则T8的值为（ ）| A． | 57 | B． | 77 | C． | 100 | D． | 126 |
分析 通过对an+1=$\frac{{a}_{n}}{1+3{a}_{n}}$两边同时取倒数，整理可知数列{$\frac{1}{{a}_{n}}$}是首项为2、公差为3的等差数列，进而利用等差数列的求和公式计算即得结论．
解答 解：∵an+1=$\frac{{a}_{n}}{1+3{a}_{n}}$，
∴$\frac{1}{{a}_{n+1}}$=$\frac{1+3{a}_{n}}{{a}_{n}}$=$\frac{1}{{a}_{n}}$+3，
又∵$\frac{1}{{a}_{1}}$=2，
∴数列{$\frac{1}{{a}_{n}}$}是首项为2、公差为3的等差数列，
∴T8=2×8+$\frac{8（8-1）}{2}$×3=100，
故选：C．
点评 本题考查数列的通项及前n项和，对表达式的灵活变形是解决本题的关键，注意解题方法的积累，属于中档题．
练习册系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1．如果复数$\frac{3-bi}{2+i}$（b∈R，i为虚数单位）的实部与虚部相等，则b的值为（ ）
| A． | 1 | B． | -6 | C． | 3 | D． | -9 |
18．已知全集U={x|-1＜x＜3}，集合A={x|x2-3x＜0}，则∁UA=（ ）
| A． | {x|-1＜x≤0} | B． | {x|-1＜x＜3} | C． | {x|0＜x＜3} | D． | {x|x≤0或x≥3} |
15．
甲、乙两厂生产的一批零件尺寸服从N（5，0.12），如果零件尺寸在（μ-3σ，μ+3σ）以外，我们就有理由认为生产中可能出现了异常情况．现从甲、乙两厂各抽取10件零件检测，尺寸如茎叶图所示：则以下判断正确的是（ ）
甲、乙两厂生产的一批零件尺寸服从N（5，0.12），如果零件尺寸在（μ-3σ，μ+3σ）以外，我们就有理由认为生产中可能出现了异常情况．现从甲、乙两厂各抽取10件零件检测，尺寸如茎叶图所示：则以下判断正确的是（ ）| A． | 甲、乙两厂生产都出现异常 | B． | 甲、乙两厂生产都正常 | ||
| C． | 甲厂生产正常，乙厂出现异常 | D． | 甲厂生产出现异常，乙厂正常 |
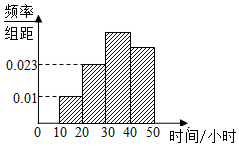为了了解学生参加体育锻炼的情况，现抽取了n名学生进行调查，结果显示这些学生每月的锻炼时间（单位：小时）都在[10，50]，其中锻炼时间在[30，50]的学生有134人，频率分布直方图如图所示，则n=（ ）