题目内容
14．设a∈R，若复数z=$\frac{a-i}{3+i}$（i是虚数单位）的实部为$\frac{1}{2}$，则复数z的虚部为（ ）| A． | $\frac{13}{30}$ | B． | -$\frac{13}{30}$ | C． | $\frac{1}{2}$ | D． | -$\frac{1}{2}$ |
分析 利用复数代数形式的乘除运算化简，由实部为$\frac{1}{2}$求得a值，进一步得到复数z的虚部．
解答 解：由z=$\frac{a-i}{3+i}$=$\frac{（a-i）（3-i）}{（3+i）（3-i）}=\frac{（3a-1）-（a+3）i}{10}$的实部为$\frac{1}{2}$，
得$\frac{3a-1}{10}=\frac{1}{2}$，解得a=2．
∴z=$\frac{1}{2}-\frac{1}{2}i$．
∴复数z的虚部为-$\frac{1}{2}$．
故选：D．
点评 本题考查复数代数形式的乘除运算，考查了复数的基本概念，是基础题．
练习册系列答案
相关题目
4．A${\;}_{5}^{2}$-C${\;}_{5}^{3}$等于（ ）
| A． | 0 | B． | -10 | C． | 10 | D． | -40 |
2．在区间[0，2]上随机取两个数x，y，则xy∈[0，2]的概率是（ ）
| A． | $\frac{1-ln2}{2}$ | B． | $\frac{3-2ln2}{4}$ | C． | $\frac{1+ln2}{2}$ | D． | $\frac{1+2ln2}{2}$ |
6．设向量$\overrightarrow{a}$，$\overrightarrow{b}$是互相垂直的两个单位向量，且|$\overrightarrow{a}$-3$\overrightarrow{b}$|=m|$\overrightarrow{a}$+$\overrightarrow{b}$|，则实数m的值为（ ）
| A． | $\sqrt{10}$ | B． | ±$\sqrt{10}$ | C． | $\sqrt{5}$ | D． | ±$\sqrt{5}$ |
3．
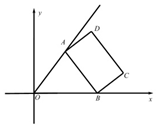已知射线OP：y=$\frac{4}{3}$x（x≥0）和矩形ABCD，AB=16，AD=9，点A、B分别在射线OP和x轴非负半轴上，则线段OD长度的最大值为（ ）
已知射线OP：y=$\frac{4}{3}$x（x≥0）和矩形ABCD，AB=16，AD=9，点A、B分别在射线OP和x轴非负半轴上，则线段OD长度的最大值为（ ）| A． | $\sqrt{337}$ | B． | 27 | C． | $\sqrt{689}$ | D． | 29 |
4．已知集合A={1，2，3}，$B=\left\{{x|\frac{2-x}{x}≥0}\right\}$，则A∩B=（ ）
| A． | {0，1，2} | B． | {1，2} | C． | {2，3} | D． | {0，2，3} |