题目内容
给定区域D:
,令点集M={(x0,y0)∈D|x0,y0∈Z},且点(x0,y0)是目标函数z=x+y在区域D上取最值的最优解},则集合M中的点最多可确定直线的条数是( )
|
| A、4条 | B、5条 | C、6条 | D、10条 |
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式组对应的平面区域,利用数形结合得到最优解的个数,即可得到结论.
解答:
 画出不等式表示的平面区域,如图.
画出不等式表示的平面区域,如图.
作出目标函数对应的直线,因为直线z=x+y与直线x+y=4平行,
故直线z=x+y过直线x+y=4上的整数点:D(4,0),C(3,1),B(2,2),A(1,3)时,直线的纵截距最大,z最大;
当直线过E(1,1)时,直线的纵截距最小,z最小,从而点集T={(4,0),(3,1),(2,2),(1,3),(1,1)},经过这5个点的直线为:
AE,BE,CE,DE,AD,一共有5条.
即M中的点共确定5条不同的直线.
故选:B.
 画出不等式表示的平面区域,如图.
画出不等式表示的平面区域,如图.作出目标函数对应的直线,因为直线z=x+y与直线x+y=4平行,
故直线z=x+y过直线x+y=4上的整数点:D(4,0),C(3,1),B(2,2),A(1,3)时,直线的纵截距最大,z最大;
当直线过E(1,1)时,直线的纵截距最小,z最小,从而点集T={(4,0),(3,1),(2,2),(1,3),(1,1)},经过这5个点的直线为:
AE,BE,CE,DE,AD,一共有5条.
即M中的点共确定5条不同的直线.
故选:B.
点评:本题主要考查线性规划的应用,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
在△ABC中,a=6,b=6,C=120°,则△ABC的面积是( )
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|
△ABC中,若C=30°,a=8,b=8
,则S△ABC等于( )
| 3 |
A、32
| ||||
B、12
| ||||
C、32
| ||||
D、16
|
 给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )
给出10个数:1,2,4,7,11…46,其规律是:第一个数是1,第二个数比第一个数大1,第三个数比第二个数大2,…以此类推,要计算这10个数的和,现已给出了该问题的程序如图所示,那么框图中判断框①处和执行框②处应分别填入( )| A、i≤10?,p=p+i-1 |
| B、i≤9?,p=p+i |
| C、i≤10?,p=p+i |
| D、i≤11?,p=p+i |
数列{an}的前n项为Sn,且Sn=2an-1,n∈N*,使得
=2a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 9 |
| n |
| A、2 | B、3 | C、4 | D、不存在 |
在△ABC中,c=18,b=12,C=60°,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
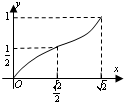
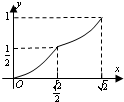
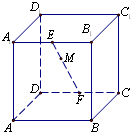 如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )
如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )