题目内容
设x,y满足约束条件
,若目标函数z=ax+by(a>0,b>0)的最小值为2,则4a+8b的最小值为( )
|
| A、2 | ||
B、2
| ||
| C、4 | ||
D、4
|
考点:简单线性规划
专题:不等式的解法及应用
分析:作出不等式对应的平面区域,利用z的几何意义确定取得最小值的条件,然后利用基本不等式即可求出4a+8b的最小值.
解答:
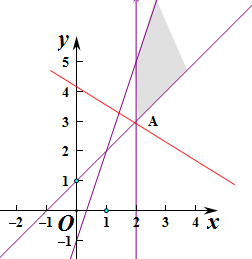 解:由z=ax+by(a>0,b>0)得y=-
解:由z=ax+by(a>0,b>0)得y=-
x+
,
∵a>0,b>0,
∴直线的斜率-
<0,
作出不等式对应的平面区域如图:
平移直线得y=-
x+
,由图象可知当直线y=-
x+
经过点A时,直线y=-
x+
的截距最小,此时z最小.
由
,解得
,即A(2,3),
此时目标函数z=ax+by(a>0,b>0)的最小值为2,
即2a+3b=2,
∴4a+8b=22a+23b≥2
=2
=2
=4,
故4a+8b的最小值为4,
故选:C.
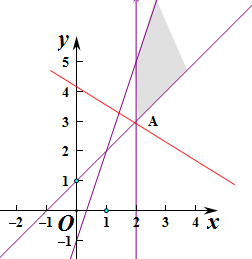 解:由z=ax+by(a>0,b>0)得y=-
解:由z=ax+by(a>0,b>0)得y=-| a |
| b |
| z |
| b |
∵a>0,b>0,
∴直线的斜率-
| a |
| b |
作出不等式对应的平面区域如图:
平移直线得y=-
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
| a |
| b |
| z |
| b |
由
|
|
此时目标函数z=ax+by(a>0,b>0)的最小值为2,
即2a+3b=2,
∴4a+8b=22a+23b≥2
| 22a•23b |
| 22a+3b |
| 22 |
故4a+8b的最小值为4,
故选:C.
点评:本题主要考查线性规划的基本应用,以及基本不等式的应用,利用数形结合求出目标函数取得最大值的条件是解决本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
一个几何体的三视图如图所示,则几何体的体积是( )


A、
| ||
B、
| ||
C、
| ||
| D、2 |
△ABC中,若C=30°,a=8,b=8
,则S△ABC等于( )
| 3 |
A、32
| ||||
B、12
| ||||
C、32
| ||||
D、16
|
数列{an}的前n项为Sn,且Sn=2an-1,n∈N*,使得
=2a1,则
+
的最小值为( )
| aman |
| 1 |
| m |
| 9 |
| n |
| A、2 | B、3 | C、4 | D、不存在 |
已知集合A={x∈R||x-1|≤2},B={x∈R|x2≤4},则A∩B=( )
| A、(-1,2) |
| B、[-1,2] |
| C、(0,2] |
| D、[-2,3] |
在△ABC中,c=18,b=12,C=60°,则cosB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、-
|
已知集合A{x|0<log3x<1},B={x|x≤2},则A∩B=( )
| A、(0,1) |
| B、(0,2] |
| C、(1,2) |
| D、(1,2] |
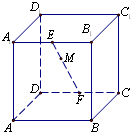 如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )
如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )