题目内容
函数f(x)=sin(2x-
)在区间[0,
]上的最小值是 .
| π |
| 4 |
| π |
| 2 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:根据题意,求出相位的范围,结合正弦函数的图象与性质可得,函数的最小值.
解答:
解:∵x∈[0,
]
∴2x-
∈[-
,
],可得f(x)=sin(2x-
)∈[-
,1]
因此,当x=0时,函数f(x)=sin(2x-
)的最小值为-
,
故答案为:-
.
| π |
| 2 |
∴2x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
| π |
| 4 |
| ||
| 2 |
因此,当x=0时,函数f(x)=sin(2x-
| π |
| 4 |
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题给出三角函数表达式,求函数在[0,
]上的最小值.着重考查了三角函数的图象与性质、函数的值域与最值等知识,属于基础题.
| π |
| 2 |

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
一个几何体的三视图如图所示,则几何体的体积是( )


A、
| ||
B、
| ||
C、
| ||
| D、2 |
设振幅、相位、初相为方程y=Asin(ωx+φ)+b(A>0)的基本量,则方程y=3sin(2x-1)+4的基本量之和为( )
| A、4 | B、2x+3 |
| C、8 | D、2x+1 |
在△ABC中,a=6,b=6,C=120°,则△ABC的面积是( )
| A、9 | ||
| B、18 | ||
C、9
| ||
D、18
|

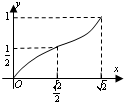
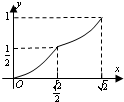
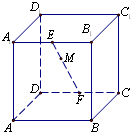 如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )
如图:正方体ABCD-A1B1C1D1的棱长为1,E,F分别是棱A1B1,CD的中点,点M是EF的动点,FM=x,过点M、直线AB的平面将正方体分成上下两部分,记下面那部分的体积为V(x),则函数V(x)的大致图象是( )