题目内容
17.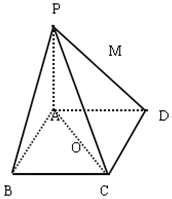 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.(1)求证:面ABM⊥面PCD;
(2)求三棱锥P-AMC的体积.
分析 (1)推导出CD⊥AD,CD⊥PA,从而CD⊥面PAD,进而AM⊥CD,再求出AM⊥MC,从而AM⊥面PCD,由此能证明面ABM⊥面PCD.
(2)三棱锥P-AMC的体积VP-AMC=VC-PAM,由此能求出结果.
解答 证明:(1)∵四边形ABCD是矩形,∴CD⊥AD,
∵PA⊥面ABCD,CD?平面ABCD,∴CD⊥PA,
∴CD⊥面PAD,∵AM?面PAD,∴AM⊥CD,
∵AC为直径的球面交PD于M,∴AM⊥MC,
∵CD与MC是面PCD内两条相交直线,
∴AM⊥面PCD,
∵AM?平面ABM,∴面ABM⊥面PCD.…6(分)
解:(2)∵PA=AD=4,等腰直角三角形PAD面积为S=8,CD=2
∴三棱锥P-AMC的体积:
VP-AMC=VC-PAM=$\frac{1}{2}$VC-PAD=$\frac{1}{2}$•$\frac{1}{3}$S•CD=$\frac{8}{3}$…12(分)
点评 本题考查面面垂直的证明,考查三棱锥的体积的求法,考查推理论证能力、运算求解能力、空间思维能力,考查函数与方程思想、化归转化思想、数形结合思想,是中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
6.已知f(x)是定义在R上的偶函数,且f(x+2)=f(x)对x∈R恒成立,当x∈[0,1]时,f(x)=2x,则$f({-\frac{9}{2}})$=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
7.复数z满足z(2+i)=1+3i,则复数z在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
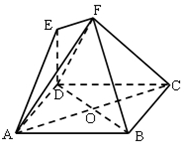 如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.
如图,多面体EF-ABCD中,四边形ABCD是菱形,AB=4,∠BAD=60°,AC,BD相交于O,EF∥AC,点E在平面ABCD上的射影恰好是线段AO的中点.