题目内容
5.动直线y=kx+4-3k与函数$f(x)=\frac{4x-11}{x-3}$的图象交于A、B两点,点P(x,y)是平面上的动点,满足$|{\overrightarrow{PA}+\overrightarrow{PB}}|=2$,则x2+y2的取值范围为[16,36].分析 确定P的轨迹方程,即可得出结论.
解答 解:y=k(x-3)+4 必经过点Q (3,4)是以新原点O'(3,4)坐标下的y'=kx'
$f(x)=\frac{4x-11}{x-3}$是以新原点O'(3,4)坐标下的x'y′1
所以交点A,B为新原点O'下的A($\frac{1}{\sqrt{k}}$,$\sqrt{k}$),B(-$\frac{1}{\sqrt{k}}$,-$\sqrt{k}$)
PA=($\frac{1}{\sqrt{k}}$-m)+($\sqrt{k}$-n)i
PB=(-$\frac{1}{\sqrt{k}}$-m)+(-$\sqrt{k}$-n)i
|PA+PB|=|-2m-2ni|=2
|m+ni|=1
即m2+n2=1 是一个圆,即P的轨迹是以(3,4)为圆心的单位圆,
∴x2+y2的取值范围为[16,36],
故答案为[16,36].
点评 本题考查轨迹方程,考查学生的计算能力,确定P的轨迹方程是关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.已知直线ax+y+1=0与(a+2)x-3y+1=0互相垂直,则实数a等于( )
| A. | 1或3 | B. | -1或3 | C. | -3或1 | D. | -3或-1 |
16.已知集合A={x|lnx≤1},B={x|-1<x<3},则集合A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x≤e} | C. | {x|0<x≤e} | D. | {x|e≤x<3} |
13.若实数x,y满足不等式组$\left\{\begin{array}{l}x+3y-3≥0\\ 2x-y-3≤0\\ x-y+1≥0\end{array}\right.$,则x+2y的最小值为( )
| A. | 2 | B. | 3 | C. | $\frac{18}{7}$ | D. | 14 |
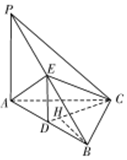 如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.
如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.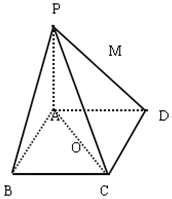 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.