题目内容
6.已知f(x)是定义在R上的偶函数,且f(x+2)=f(x)对x∈R恒成立,当x∈[0,1]时,f(x)=2x,则$f({-\frac{9}{2}})$=( )| A. | $\frac{1}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | 1 |
分析 先确定函数f(x)的周期为2,再利用函数f(x)是定义在R上的偶函数,当x∈[0,1]时,f(x)=2x,即可得出结论.
解答 解:∵f(x+2)=f(x)对x∈R恒成立,
∴f(x)的周期为2,(x)是定义在R上的偶函数,
∴$f({-\frac{9}{2}})$=f(-$\frac{1}{2}$)=f($\frac{1}{2}$)
∵当x∈[0,1]时,f(x)=2x,
∴f($\frac{1}{2}$)=$\sqrt{2}$,
故选:B.
点评 本题考查抽象函数及其应用,考查函数的周期性,属于中档题.

练习册系列答案
相关题目
16.已知集合A={x|lnx≤1},B={x|-1<x<3},则集合A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x≤e} | C. | {x|0<x≤e} | D. | {x|e≤x<3} |
16.已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中$φ∈(0,\frac{π}{2})$,则函数g(x)=cos(2x-φ)的图象( )
| A. | 关于点$(\frac{π}{12},0)$对称 | |
| B. | 关于轴$x=-\frac{5π}{12}$对称 | |
| C. | 可由函数f(x)的图象向右平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
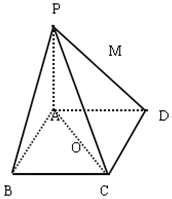 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.