题目内容
7.极坐标方程ρcosθ=sin2θ,表示曲线的图形是一条直线和一个圆.分析 极坐标方程转化为cosθ=0或ρ=2sinθ,由此能求出结果.
解答 解:∵ρcosθ=sin2θ=2sinθcosθ,
∴cosθ=0或ρ=2sinθ,
∴极坐标方程ρcosθ=sin2θ表示曲线的图形是一条直线和一个圆.
故答案为:一条直线和一个圆.
点评 本题考查极坐标方程表示的曲线图形的判断,考查参数方程、直角坐标方程、极坐标方程互化公式的应用,考查运算求解能力、转化化归思想,是中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
9.已知直线ax+y+1=0与(a+2)x-3y+1=0互相垂直,则实数a等于( )
| A. | 1或3 | B. | -1或3 | C. | -3或1 | D. | -3或-1 |
19.设函数f(x)=ex-e-x,g(x)=lg(mx2-x+$\frac{1}{4}$),若对任意x1∈(-∞,0],都存在x2∈R,使得f(x1)=g(x2),则实数m的最小值为( )
| A. | -$\frac{1}{3}$ | B. | -1 | C. | -$\frac{1}{2}$ | D. | 0 |
16.已知集合A={x|lnx≤1},B={x|-1<x<3},则集合A∩B=( )
| A. | {x|-1<x<3} | B. | {x|-1<x≤e} | C. | {x|0<x≤e} | D. | {x|e≤x<3} |
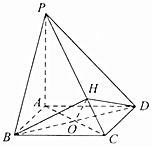 如图,四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,AC交BD于O,H为线段PC上一点.
如图,四棱锥P-ABCD的底面是边长为2的正方形,PA⊥平面ABCD,AC交BD于O,H为线段PC上一点.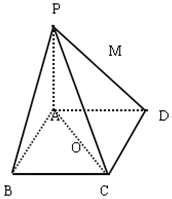 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.