题目内容
13.已知函数f(x)=ax4+x3+bx2+2x+c(其中a、b、c为常数)为奇函数,f′(x)是函数f(x)的导函数,则f′(2)=6.分析 先根据奇函数的性质,求出a=0,b=0,c=0,继而得到f(x)=x3+2x,再求导,代值计算即可.
解答 解:f(x)=ax4+x3+bx2+2x+c(其中a、b、c为常数)为奇函数,
∴f(-x)=-f(x),
∴a(-x)4-x3+b(-x)2-2x+c=-ax4-x3-bx2-2x-c,
∴ax4+bx2+2c=0
∵x在定义域内任意取值,要等式恒成立,只有a=0,b=0,c=0,
∴f(x)=x3+2x,
∴f′(x)=2x+2,
∴f′(2)=2×2+2=6,
故答案为:6.
点评 本题考查了奇函数的性质,以及导数的运算法则,属于中档题.

练习册系列答案
相关题目
4.在如图程序框图中,已知:f0(x)=(x+9)ex,则输出的是( )
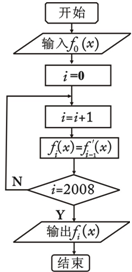

| A. | 2019ex+xex | B. | 2018ex+xex | C. | 2017ex+xex | D. | 2016ex+xex |
8.复数$\frac{-i}{3+i}$在复平面上对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
2.要得到函数y=2sin(2x+$\frac{2π}{3}$)的图象,需要将函数y=2sin2x的图象( )
| A. | 向左平移$\frac{2π}{3}$个单位 | B. | 向右平移$\frac{2π}{3}$个单位 | ||
| C. | 向左平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{3}$个单位 |