题目内容
函数y=x2-6x+1，x∈[2，5]的值域是（ ）
| A、[-8，-4] |
| B、[-8，-4） |
| C、[-7，-4] |
| D、[-7，-4） |
考点：二次函数在闭区间上的最值
专题：函数的性质及应用
分析：求出二次函数的对称轴，研究函数在x∈[1，5]的单调性，解出最值，写出值域即可．
解答：
解：函数y=x2-6x+1的对称轴是x=3，由二次函数的性质知，函数在[2，3]上是减函数，在[3，5]上函数是增函数
又x=2，y=-7，
x=3，y=-8
x=5，y=-4
故函数的值域是[-8，-4]．
故选：A．
又x=2，y=-7，
x=3，y=-8
x=5，y=-4
故函数的值域是[-8，-4]．
故选：A．
点评：本题考查二次函数在闭区间上的最值，解答本题关键是根据二次函数的性质判断出函数在何处取到最值，二次函数在闭区间上最值在高中数学中应用十分广泛，一些求最值的问题最后往往归结到二次函数的最值上来．
练习册系列答案
综合自测系列答案
相关题目
从2009名学生中选取50名学生参加数学竞赛，若采用下面的方法选取：先用简单随机抽样从2009人中剔除9人，剩下的2000人再按系统抽样的方法抽取50人，则在2009人中，每人入选的概率（ ）
| A、不全相等 | ||
| B、均不相等 | ||
C、都相等，且为
| ||
D、都相等，且为
|
已知函数f（x）=
，则函数f（1）的值为（ ）
|
| A、-1 | B、0 | C、1 | D、4 |
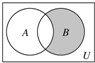已知全集U=N，A={0，1，2}，B={y|y=2x，x∈A}，则图中的阴影部分所表示的集合等于（ ）| A、{0} | B、{2} |
| C、{4} | D、{2，4} |
已知函数f（x）=2cos（2x+φ），（|φ|＜| π |
| 2 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
函数f（x）=x-4+log2x的零点所在的区间是（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
若x0是方程式lgx+x=2的解，则x0属于区间（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |