题目内容
5.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=($\frac{1}{2}$)x,那么f(-2),f(-$\frac{π}{2}$),f(3)的大小关系是( )| A. | f(-$\frac{π}{2}$)>f(-2)>f(3) | B. | f(-$\frac{π}{2}$)>f(3)>f(-2) | C. | f(3)>f(-$\frac{π}{2}$)>f(-2) | D. | f(3)$>f(-2)>f(-\frac{π}{2})$ |
分析 根据函数奇偶性的关系结合指数函数的单调性的性质进行判断即可.
解答 解:∵f(x)是定义在R上的偶函数,
∴么f(-2)=f(2),f(-$\frac{π}{2}$)=f($\frac{π}{2}$),
∵当x≥0时,f(x)=($\frac{1}{2}$)x,
∴此时函数f(x)为减函数,
∵$\frac{π}{2}$<2<3,
∴f($\frac{π}{2}$)>f(2)>f(3),
即f(-$\frac{π}{2}$)>f(-2)>f(3),
故选:A
点评 本题主要考查函数值的大小比较,根据函数奇偶性和单调性的关系进行转化求解是解决本题的关键.

练习册系列答案
相关题目
14.已知向量$\overrightarrow{a}$=(2,tanθ),$\overrightarrow{b}$=(1,-1),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则tan($\frac{π}{4}$+θ)等于( )
| A. | 2 | B. | -3 | C. | -1 | D. | -$\frac{1}{3}$ |
15.若集合U={1,2,3,4,5,6},A={2,5,6},B={1,3,5},那么(∁UA)∩B=( )
| A. | {5} | B. | {1,3} | C. | {2,6} | D. | {1,3,4,5,6} |
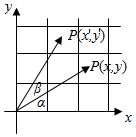 如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.