题目内容
16.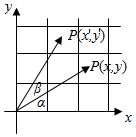 如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
如图,设OP与x轴的正方向的夹角为α,OP'与OP的夹角为β,现将OP绕O点旋转到与OP'重合,旋转角β=$\frac{π}{6}$,则这个旋转变换对应的矩阵为$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
分析 根据矩阵的线性变换,即可求得旋转变换对应的矩阵.
解答 解:由二阶矩阵的线性变换性质可得:$[\begin{array}{l}{cosβ}&{-sinβ}\\{sinβ}&{cosβ}\end{array}]$$[\begin{array}{l}{x}\\{y}\end{array}]$=$[\begin{array}{l}{xcosβ-ysinβ}\\{xsinβ+ycosβ}\end{array}]$,
则旋转变换对应的矩阵A=$[\begin{array}{l}{cosβ}&{-sinβ}\\{sinβ}&{cosβ}\end{array}]$=$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$,
故答案为:$[\begin{array}{l}{\frac{\sqrt{3}}{2}}&{-\frac{1}{2}}\\{\frac{1}{2}}&{\frac{\sqrt{3}}{2}}\end{array}]$.
点评 本题考查矩阵的线性变换的简单应用,考查转化思想,属于基础题.

练习册系列答案
相关题目
11.已知4张卡片上分别写着数字1,2,3,4,甲、乙两人等可能地从这4张卡片中选择1张,则他们选择同一张卡片的概率为( )
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
11.已知cos($\frac{π}{4}$+α)=-$\frac{3}{5}$,且α是第三象限角,则cos($\frac{π}{4}$+2α)的值为( )
| A. | $\frac{31}{50}$$\sqrt{2}$ | B. | $\frac{17}{50}$$\sqrt{2}$ | C. | -$\frac{17}{50}$$\sqrt{2}$ | D. | -$\frac{31}{50}$$\sqrt{2}$ |
1. 一个如图放置的三棱柱的底面是正三角形,侧棱与底面垂直,它的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积为( )
一个如图放置的三棱柱的底面是正三角形,侧棱与底面垂直,它的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积为( )
 一个如图放置的三棱柱的底面是正三角形,侧棱与底面垂直,它的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积为( )
一个如图放置的三棱柱的底面是正三角形,侧棱与底面垂直,它的左视图是边长为$\sqrt{3}$的正方形,则它的外接球的表面积为( )| A. | 8π | B. | $\frac{25π}{3}$ | C. | 9π | D. | $\frac{28π}{3}$ |
8.已知在三棱锥P-ABC中,PA=PB=PC=1,AB=$\sqrt{2}$,AB⊥BC,平面PAB⊥平面ABC,若三棱锥的顶点在同一球面上,则该球的表面积为( )
| A. | $\frac{{\sqrt{3}π}}{2}$ | B. | 3π | C. | $\frac{{\sqrt{2}π}}{3}$ | D. | 2π |
5.已知f(x)是定义在R上的偶函数,当x≥0时,f(x)=($\frac{1}{2}$)x,那么f(-2),f(-$\frac{π}{2}$),f(3)的大小关系是( )
| A. | f(-$\frac{π}{2}$)>f(-2)>f(3) | B. | f(-$\frac{π}{2}$)>f(3)>f(-2) | C. | f(3)>f(-$\frac{π}{2}$)>f(-2) | D. | f(3)$>f(-2)>f(-\frac{π}{2})$ |
6.下列函数中,值域为(0,+∞)的是( )
| A. | sinx+cosx | B. | $y=\sqrt{1-{2^x}}$ | C. | y=2x2+x+1 | D. | $y={2^{-\frac{x}{2}}}$ |
 如图,利用随机模拟的方法可以估计图中曲线y=f(x)与两直线x=2及y=0所围成的阴影部分的面积S:①先从区间[0,2]随机产生2N个数x1,x2,…xn,y1,y2,…yn,构成N个数对,(x1,y1),(x2,y2),…(xn,yn);②统计满足条件y<f(x)的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=300,则据此可估计S的值为1.2.
如图,利用随机模拟的方法可以估计图中曲线y=f(x)与两直线x=2及y=0所围成的阴影部分的面积S:①先从区间[0,2]随机产生2N个数x1,x2,…xn,y1,y2,…yn,构成N个数对,(x1,y1),(x2,y2),…(xn,yn);②统计满足条件y<f(x)的点(x,y)的个数N1,已知某同学用计算器做模拟试验结果,当N=1000时,N1=300,则据此可估计S的值为1.2.