题目内容
以边长1的正方形的一边所在直线为旋转轴将正方形旋转一周，所得圆柱的侧面积等于 ．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：边长为1的正方形，绕其一边所在直线旋转一周，得到的几何体为圆柱，从而可求圆柱的侧面积．
解答：
解：边长为1的正方形，绕其一边所在直线旋转一周，得到的几何体为圆柱，
则所得几何体的侧面积为：1×2π×1=2π，
故答案为：2π
则所得几何体的侧面积为：1×2π×1=2π，
故答案为：2π
点评：本题是基础题，考查旋转体的侧面积的求法，考查计算能力．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知曲线C：
-
=1的左、右顶点分别为A1，A2，点P在C上且直线PA2斜率的取值范围是[-2，-1]，那么直线PA1斜率的取值范围是（ ）
| x2 |
| 4 |
| y2 |
| 6 |
A、[-1，-
| ||||
B、[-
| ||||
C、[-1，-
| ||||
D、[-
|
已知函数f（x）=
，若a，b，c互不相等，且f（a）=f（b）=f（c），则abc的取值范围是（ ）
|
| A、（0，2016） |
| B、（0，2016] |
| C、（0，504） |
| D、（0，504] |
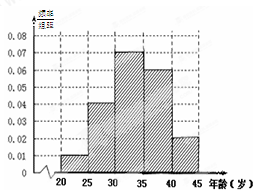上海世博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．根据如图所示的频率分布直方图，估计这507个画师中年龄不超过30岁的人数约
