题目内容
已知数列{an}满足a1+3a2+32a3+…+3n-1an=n
(1)求an
(2)设bn=2an求数列{bn}的前n项和Sn.
(1)求an
(2)设bn=2an求数列{bn}的前n项和Sn.
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)由于数列{an}满足a1+3a2+32a3+…+3n-1an=n,可得当n≥2时,3n-1an=n-(n-1)=1,即可得出an.
(2)bn=2an=
,利用等比数列的前n项和公式即可得出.
(2)bn=2an=
| 2 |
| 3n-1 |
解答:
解:(1)∵数列{an}满足a1+3a2+32a3+…+3n-1an=n,
∴当n≥2时,a1+3a2+32a3+…+3n-2an-1=n-1,
∴两式作差得3n-1an=n-(n-1)=1,
∴an=
,
当n=1时,a1=1也成立.
∴an=
.
(2)bn=2an=
,
∴Sn=2+
+
+…+
=2×
=3-
.
∴当n≥2时,a1+3a2+32a3+…+3n-2an-1=n-1,
∴两式作差得3n-1an=n-(n-1)=1,
∴an=
| 1 |
| 3n-1 |
当n=1时,a1=1也成立.
∴an=
| 1 |
| 3n-1 |
(2)bn=2an=
| 2 |
| 3n-1 |
∴Sn=2+
| 2 |
| 3 |
| 2 |
| 32 |
| 2 |
| 3n-1 |
1-
| ||
1-
|
| 1 |
| 3n-1 |
点评:本题考查了等比数列的通项公式及其前n项和公式、递推式的应用,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
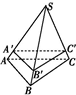 已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<
已知正棱锥S-ABC的底面边长为4,高为3,在正棱锥内任取一点P,使得VP-ABC<| 1 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
设f(x)是定义在(0,+∞)上的增函数,当a,b∈(0,+∞)时,均有f(a•b)=f(a)+f(b),已知f(2)=1.求:
(1)f(1)和f(4)的值;
(2)不等式f(x2)<2f(4)的解集.
(1)f(1)和f(4)的值;
(2)不等式f(x2)<2f(4)的解集.
某程序框图如图所示,若输出的S=57,则判断框内应填( )


| A、k>4? | B、k>5? |
| C、k>6? | D、k>7? |
若x满足不等式|2x-1|≤1,则函数y=(
)x的值域为( )
| 1 |
| 2 |
A、[0,
| ||
B、(-∞,
| ||
| C、(0,1] | ||
D、[
|