题目内容
设变量x,y满足
,则z=x+y的最大值是 .
|
考点:简单线性规划
专题:不等式的解法及应用
分析:画出约束条件不是的可行域,判断目标函数经过的点,求出最大值.
解答:
 解:由约束条件
解:由约束条件
画出可行域如图所示,
,可得
则目标函数z=x+y在点A(2,1)取得最大值,
代入得x+y=3,故x+y的最大值为3.
故答案为:3.
 解:由约束条件
解:由约束条件
|
|
|
则目标函数z=x+y在点A(2,1)取得最大值,
代入得x+y=3,故x+y的最大值为3.
故答案为:3.
点评:本题考查线性规划的应用,画出约束条件的可行域以及找出目标函数经过的点是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
为了得到函数y=sin(2x+
),x∈R的图象,只需将函数y=sin2x,x∈R图象上所有的点( )
| π |
| 4 |
A、向左平行移动
| ||
B、向右平行移动
| ||
C、向左平行移动
| ||
D、向右平行移动
|
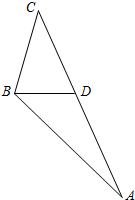 近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4
近日我渔船编队在钓鱼岛附近点A周围海域作业,在B处的海监15船测得A在其南偏东45°方向上,测得渔政船310在其北偏东15°方向上,且与B的距离为4