题目内容
1．在两个学习基础相当的班级实行某种教学措施的实验，测试结果见表，则实验效果与教学措施（ ）| 优、良、中 | 差 | 总计 | |
| 实验班 | 48 | 2 | 50 |
| 对比班 | 38 | 12 | 50 |
| 总计 | 86 | 14 | 100 |
| A． | 有关 | B． | 无关 | C． | 关系不明确 | D． | 以上都不正确 |
分析 根据所给的观测值，同临界值表中的临界值进行比较，可得结论．
解答 解：∵k2=$\frac{100×（48×12-38×2）^{2}}{86×14×50×50}$≈8.306＞7.879，
P（k2＞7.879）=0.005，
∴在犯错误的概率不超过0.005的前提下认为实验效果与教学措施有关．
故选：A．
点评 本题考查独立性检验的应用，本题解题的关键是正确理解临界值对应的概率的意义．
练习册系列答案
相关题目
函数y=2sinπx（x∈R）的部分图象如图所示，设O为坐标原点，P是图象的最高点，B是图象与x轴的交点，则tan∠OPB的值为$\frac{16}{3}$．
10．
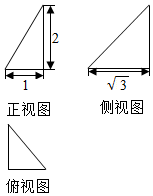某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）
某几何体的三视图如图所示，则该几何体外接球的表面积为（ ）| A． | $\frac{25π}{4}$ | B． | $\frac{25π}{8}$ | C． | 12π | D． | 8π |
9．
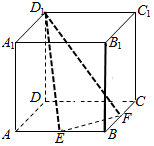如图，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，过点D1、E、F的截面将正方体分割成两个部分，记这两个部分的体积分别为V1、V2（V1＜V2），则V1：V2=（ ）
如图，正方体ABCD-A1B1C1D1中，E、F分别是AB、BC的中点，过点D1、E、F的截面将正方体分割成两个部分，记这两个部分的体积分别为V1、V2（V1＜V2），则V1：V2=（ ）| A． | $\frac{1}{3}$ | B． | $\frac{3}{5}$ | C． | $\frac{25}{47}$ | D． | $\frac{7}{9}$ |
16．向量$\vec a=（{-1，1}）$，$\vec b=（{1，0}）$，若$（{\vec a-\vec b}）⊥（{2\vec a+λ\vec b}）$，则λ=（ ）
| A． | 2 | B． | -2 | C． | -3 | D． | 3 |
6．已知i是虚数单位，若$z（{1-\frac{1}{2}i}）=\frac{1}{2}i$，则|Z|=（ ）
| A． | 1 | B． | $\frac{{\sqrt{3}}}{2}$ | C． | $\sqrt{5}$ | D． | $\frac{{\sqrt{5}}}{5}$ |
13．如图，已知四边形ABCD为矩形，PA⊥平面ABCD，下列结论中不一定正确的是（ ）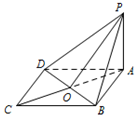
| A． | PD⊥CD | B． | BD⊥平面PAO | C． | PB⊥CB | D． | BC∥平面PAD |
10．已知x，y满足约束条件$\left\{\begin{array}{l}x-y-2≤0\\ x+2y-5≥0\\ y-2≤0\end{array}\right.$，则z=$\frac{y+1}{x+1}$的范围是（ ）
| A． | $[\frac{1}{3}，2]$ | B． | $[-\frac{1}{2}，\frac{1}{2}]$ | C． | $[\frac{1}{2}，\frac{3}{2}]$ | D． | $[\frac{3}{2}，\frac{5}{2}]$ |
11．某研究所计划利用“神七”宇宙飞船进行新产品搭载实验，计划搭载若干件新产品A、B，该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排，通过调查，有关数据如表：
如何安排这两种产品的件数进行搭载，才能使总预计收益达到最大，最大收益是多少？
| 每件产品A | 每件产品B | ||
| 研制成本、搭载 费用之和（万元） | 20 | 30 | 计划最大资金额 300万元 |
| 产品重量（千克） | 10 | 5 | 最大搭载重量110千克 |
| 预计收益（万元） | 80 | 60 |