题目内容
5.已知Rt△ABC的周长为定值l,则它的面积最大值为$\frac{3-2\sqrt{2}}{4}$.分析 设三边法不为a,b,c,c为斜边,则c2=a2+b2.由a+b+c=1,可得a2+b2=(1-a-b)2,化为:1-2a-2b+2ab=0,变形1+2ab=2(a+b),再利用基本不等式的性质与三角形面积计算公式即可得出.
解答 解:设三边为a,b,c,c为斜边,则c2=a2+b2.
∵a+b+c=1,
∴a2+b2=(1-a-b)2,化为:
1-2a-2b+2ab=0,
∴1+2ab=2(a+b)≥4$\sqrt{ab}$,化为:$2(\sqrt{ab})^{2}$-4$\sqrt{ab}$+1≥0,解得$\sqrt{ab}$≥$\frac{2+\sqrt{2}}{2}$,(舍去),
或$\sqrt{ab}$≤$\frac{2-\sqrt{2}}{2}$,即ab≤$(\frac{2-\sqrt{2}}{2})^{2}$=$\frac{3-2\sqrt{2}}{2}$.当且仅当a=b=$\frac{2-\sqrt{2}}{2}$时取等号.
∴它的面积最大值=$\frac{1}{2}$ab=$\frac{3-2\sqrt{2}}{4}$.
故答案为:$\frac{3-2\sqrt{2}}{4}$.
点评 本题考查了基本不等式的性质与三角形面积计算公式、勾股定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
16.已知函数$f(x)=cosx+{2^x}-\frac{1}{2}(x<0)$与g(x)=cosx+log2(x+a)图象上存在关于y轴对称的点,则a的取值范围是( )
| A. | $(-∞,-\sqrt{2})$ | B. | $(-∞,-\frac{{\sqrt{2}}}{2})$ | C. | $(-\sqrt{2},\frac{{\sqrt{2}}}{2})$ | D. | $(-∞,\sqrt{2})$ |
20.圆心在直线2x-y-6=0上的圆C与y轴交于两点A(0,-5),B(0,-3),则圆C的方程是( )
| A. | (x-1)2+(y+4)2=2 | B. | (x+1)2+(y-4)2=2 | C. | (x-1)2+(y-4)2=2 | D. | (x+1)2+(y+4)2=2 |
17.已知抛物线x2=2px(p>0)经过点线$M({\frac{1}{2},2})$,则它的准线方程为( )
| A. | $y=-\frac{1}{32}$ | B. | B | C. | C | D. | D |
14.有一个几何体的三视图及其尺寸如下(单位:cm),其侧视图和主视图是全等的三角形,则该几何体的表面积为( )


| A. | 12cm2 | B. | 15πcm2 | C. | 24πcm2 | D. | 36πcm2 |
15.已知a∈R,命题“?x∈(0,+∞),等式lnx=a成立”的否定形式是( )
| A. | ?x∈(0,+∞),等式lnx=a不成立 | B. | ?x∈(-∞,0),等式lnx=a不成立 | ||
| C. | ?x0∈(0,+∞),等式lnx0=a不成立 | D. | ?x0∈(-∞,0),等式lnx0=a不成立 |
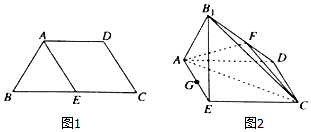 已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点.
已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是BC的中点,将△BAE沿着AE翻折成△B1AE,使平面B1AE⊥平面ABCD,F,G分别为B1D,AE的中点. 已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.
已知函数$f(x)=2sin(2x+φ)\;(|φ|<\frac{π}{2})$部分图象如图所示.