题目内容
4.下列各组向量共面的是( )| A. | $\overrightarrow a=(1,0,-1),\overrightarrow b=(1,1,0),\overrightarrow c=(0,1,1)$ | B. | $\overrightarrow a=(1,0,0),\overrightarrow b=(0,1,-1),\overrightarrow c=(0,0,1)$ | ||
| C. | $\overrightarrow a=(1,1,1),\overrightarrow b=(1,-1,0),\overrightarrow c=(1,0,1)$ | D. | $\overrightarrow a=(1,1,0),\overrightarrow b=(1,0,1),\overrightarrow c=(0,1,1)$ |
分析 利用向量共面定理可知:如果存在实数m,n使得$\overrightarrow{a}=m\overrightarrow{b}+n\overrightarrow{c}$成立,则向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面.即可判断出.
解答 解:利用向量共面定理可知:如果存在实数m,n使得$\overrightarrow{a}=m\overrightarrow{b}+n\overrightarrow{c}$成立,则向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$共面.
经过判定:对于A:$\overrightarrow{a}$=$\overrightarrow{b}-\overrightarrow{c}$,而B,C,D不满足向量共面定理.
故选:A.
点评 本题考查了向量共面定理,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
15.函数f(x)=ax2-2x+3在(-∞,1]上是减函数,则实数a的取值范围是( )
| A. | (-∞,1] | B. | (0,1] | C. | [1,+∞) | D. | [0,1] |
16.已知函数f(x)=($\frac{1}{2}$)x-1和g(x)=-10x+20,则二者图象的交点的横坐标所属区间为( )
| A. | (0,1) | B. | (1,2) | C. | (2,3) | D. | (3,4) |
13.某几何体的三视图如图所示(单位:cm),则该几何体的表面积等于( )


| A. | 8πcm2 | B. | 7πcm2 | C. | 6πcm2 | D. | 5πcm2 |
13.椭圆3x2+2y2=1的焦点坐标是( )
| A. | $(0,-\frac{{\sqrt{6}}}{6}),(0,\frac{{\sqrt{6}}}{6})$ | B. | $(-\frac{{\sqrt{6}}}{6},0),(\frac{{\sqrt{6}}}{6},0)$ | C. | (-1,0),(1,0) | D. | (0,-1)、(0,1) |
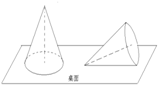 用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.
用一个半径为10厘米的半圆纸片卷成一个最大的无底圆锥,放在水平桌面上,被一阵风吹倒,如图,则它的最高点到桌面的距离为5$\sqrt{3}$cm.