题目内容
16.在平面向量$\overrightarrow{a}$,$\overrightarrow{b}$中,已知$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(2,y).如果$\overrightarrow{a}$•$\overrightarrow{b}$=5,那么y=1;如果|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,那么y=-$\frac{2}{3}$.分析 代入数量积公式计算.
解答 解:∵$\overrightarrow{a}$•$\overrightarrow{b}$=5,∴1×2+3y=5,解得y=1.
∵|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$-$\overrightarrow{b}$|,∴$\overrightarrow{a}$⊥$\overrightarrow{b}$,∴1×2+3y=0,解得y=-$\frac{2}{3}$.
故答案为$1;-\frac{2}{3}$.
点评 本题考查了平面向量的数量积运算,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.当x→0时,下列4个无穷小量中比其它3个更高阶的无穷小量是( )
| A. | 1n(1+x) | B. | ex-1 | C. | tanx-sinx | D. | 1-cosx |
1.已知集合A={1,2,m},B={3,4}.若A∩B={3},则实数m=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
5.已知函数f(x)的图象如图所示,则f(x)的解析式可能是( )
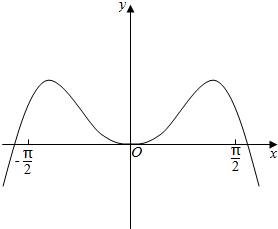

| A. | x2cosx | B. | sinx2 | C. | xsinx | D. | x2-$\frac{1}{6}$x4 |
6.数列{an}中an=$\frac{1}{{n}^{2}}$(n∈N*),f(n)=(1-a3)(1-a4)…(1-an),f(n)=( )
| A. | $\frac{2n+2}{{n}^{2}}$ | B. | $\frac{n+5}{3n}$ | C. | $\frac{2n+2}{3n}$ | D. | $\frac{2n+2}{2n+3}$ |